Codeforces 1237E Perfect Balanced Binary Search Tree

题目链接

Observations

含有 $n$ 个点且 key（以下也称 key 为「权值」）是 1 到 $n$ 的 BST 具有下列性质：

若 $k$ 是一个非根叶子且是个左儿子，则 $k$ 的父亲是 $k+1$ 。

证明：假设 $k$ 的父亲是 $p$ 且 $p \ne k + 1$，则 $p > k + 1$；显然 $k + 1$ 不可能是 $k$ 的祖先。
设 $k$ 和 $k + 1$ 的最近公共祖先是 $t$，则有 $k < t < k + 1$ 或者 $ k + 1 < t < k$，矛盾！

同理可证，若 $k$ 是一个非根的叶子且是个右儿子，则 $k$ 的父亲是 $k - 1$ 。

注：上述性质也可以从「BST 的任意子树中 key 都是连续的」这个性质推出。

---

从而可以得出，striped BST 的所有叶子都是左儿子。

---

perfectly balanced BST 只有最后一层可能不满，其他层都是满的。

$n$ 个点的 perfectly balanced BST 的高度是 $\floor{\log n}$ 。

---

Q：是否只要满足

• 所有叶子节点都是左儿子
• 除了最后一层，每层都是满的

就一定存在一种填充权值的方案使得这棵树是一棵 perfectly balanced striped BST？
A：不是。

递推

有根树具有天然的递归结构。

容易看出

1. perfectly balanced striped BST 的任意子树也是 perfectly balanced striped BST。
2. 可以把任意一棵 $k$ 个点的子树的权值范围变成 $1$ 到 $k$ 且保持其为 striped BST。换言之，我们只需要考虑权值从 1 开始的情形。这里用到了 BST 的任意子树中 key 值连续的性质。

欲求 $n$ 个点的 perfectly balanced striped BST 的数量，可以枚举根节点的权值。一棵子树内的权值必定是连续的，根节点的权值确定后，根的左右子树的节点数就确定了。设根节点的权值是 $r$，则左子树中有 $r - 1$ 个点，权值范围是 $1$ 到 $r - 1$；右子树中有 $n - r$ 个点，权值范围是 $r + 1$ 到 $n$ 。左子树的根的权值的奇偶性须跟 $r$ 不同，换言之，左子树的根的权值须与其中点的个数的奇偶性相同。右子树的根节点的权值须跟 $r$ 同奇偶。设右子树的根的权值是 $w$；把右子树的权值平移到 $1$ 到 $n - r$ 以后，$w$ 对应于 $w - r$，$w$ 与 $r$ 同奇偶意味着 $w - r$ 是偶数。

总而言之，一个 $n$ 个节点，权值是 $1, 2, \dots, n$ 的 perfectly balanced striped BST 能作为根的左子树的必要条件是其根的权值与其中节点数同奇偶；能作为根的右子树的必要条件是其根的权值是偶数。

设 $T_1, T_2$ 是两棵 perfectly balanced striped BST。
若以 $T_1$ 为左子树，$T_2$ 为右子树能组合成一棵新的 perfectly balanced striped BST，则 $T_1, T_2$ 除了需要满足上述条件外，还需满足二者高度相等或二者高度相差 $1$ 且高度较小者是完美二叉树。

注：从上一节的分析可知，子树是完美二叉树的情形，只有一个点的树这一种情况；即下图所示的情形

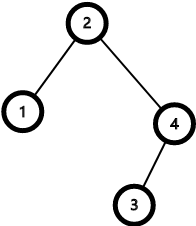
不难注意到，(i) 组合成的新树可以作为左子树当且仅当新树的右子树中有偶数个点；(ii) 组合成的新树可作为右子树当且仅当新树的左子树中有奇数个点。

对于 $n \ge 5$，$n$ 个点的 perfectly balanced striped BST 的根节点的左右两棵子树的高度都不小于 1 。从上一节得出的两必要条件可以推出，此时左右两子树都不是完美二叉树，这意味着二者高度相同。设 $n$ 个点的 perfectly balanced BST 的高度是 $h$，则根的左右子树的高度都是 $h - 1$ 。

考虑高度为 $i$（$i \ge 2$）的 perfectly balanced striped BST，将其中能作为高度为 $i + 1$ 的 perfectly balanced striped BST 的根的左子树和右子树的 perfectly balanced striped BST 的「信息」分别放到两个列表 $L_i$ 和 $R_i$ 中。信息表为有序二元组：(节点数, 方案数)。
从 $L_i$ 中任取一元素 $\ell$，从 $R_i$ 中任取一元素 $r$，通过组合 $\ell, r$ 来构造 $L_{i + 1}$ 和 $R_{i + 1}$ 。

$L_{-1} = \{(0, 1)\}, R_{-1} = \{(0, 1)\}$；$(0, 1)$ 对应于空图
$L_0 = \{ (1, 1)\}, R_0 = \emptyset$；
$L_1 = \{(2, 1)\}, R_1 = \{(2, 1)\}$
$L_2 = \{(4, 1), (5, 1)\}, R_2 = \{(4, 1)\}$；$(4, 1)$ 是由 $L_0$ 中的 $(1,1)$ 和 $L_1$ 中的 $(2, 1)$ 组合得到的，上图即对应于 $(4, 1)$。
$L_3 = \{(9, 1), (10, 1)\}, R_3 = \{(10, 1)\}$
$L_4 = \{(20, 1), (21, 1) \}, R_4 = \{(20, 1)\}$
$\vdots$

从以上分析中不难看出，给定 $n$，number of perfectly balanced striped binary search trees with $n$ vertices that have distinct integer keys between $1$ and $n$, inclusive 要么是 0 要么是 1。