区间DP小结 及例题分析：P1880 [NOI1995]石子合并，P1063 能量项链

区间类动态规划

一.基本概念

区间类动态规划是线性动态规划的拓展，它在分阶段划分问题时，与阶段中元素出现的顺序和由前一阶段的那些元素合并而来由很大的关系。例如状态f [ i ][ j ]，它表示以已合并的次数为阶段，以区间的左端点 i 为状态，它的值取决于第 i 个元素和第 j 个元素断开的位置 k，即 f [ i ][ k ] + f [ k+1 ][ j ]的值。这一类型的动态规划，阶段特征非常明显，求最优值时需要预先设置阶段内的区间统计值，还要以动态规划的起始位置来判断。 

区间类动态规划的特点：

合并：即将两个或多个部分进行整合，当然也可以反过来，也就是对一个问题分解成两个或多个部分。

特征：能将问题分解成为两两合并的形式。

求解：对整个问题设最优值，枚举合并点，将问题分解成左右两个部分，最后合并左右两个部分的最优值得到原问题的最优值。有点类似分治算法的解题思想。

    for(int len=;len<=n;len++)                       //枚举区间长度
       for(int i=;i<=n-len+;i++)                    //枚举左端点
       {
              j=i+len-;                                 //右端点
              for(int k=i;k<j;k++)                       //枚举中间断点
              {
              f[i][j]=max(f[i][k]+f[k+][j],f[i][j]);    //最大值状态转移方程
              f[i][j]=min(f[i][k]+f[k+][j],f[i][j]);    //最小值状态转移方程
              }
       }

二.例题分析

P1880 [NOI1995]石子合并

首先很多人第一眼看这个题会误以为是贪心，毕竟样例贪心分析也是如此，但其实不是贪心，而是区间DP；

正解：

若最初的第 l 堆石子和第 r 堆石子被合并成一堆，则说明 l~r 之间的每堆石子也已经被合并，这样 l 和 r 才有可能相邻。因此，在任意时刻，任意一堆石子均可以用一个闭区间 [ l，r ]来描述，表示这堆石子是由最初的第 l~r 堆石子合并而成的，其重量为∑ a_i （l <= i <= r）。另外，一定存在一个整数 k （l <=k <r）在这堆石子形成之前，先有第 l~k 堆石子（闭区间 [ l，k ]）被合并成一堆，第 k+1~r 堆石子（闭区间 [ k+1，r ]）被合并成一堆，然后这两堆石子在合并成 [ l，r ]。

对应到动态规划中，就意味着两个长度较小的区间上的信息向一个更长区间发生了转移，划分点 k 就是转移的决策。自然地，应该把区间长度len 作为DP的阶段。不过，区间长度可以由左端点和右端点表示，即len=r - l + 1。本着动态规划“选择最小的能覆盖状态空间的维度集合”的思想，我们可以只用左右端点表示DP的状态。

设 sum [ i ]表示从1堆石子到第 i 堆石子数总和，sum [ i ] = a[ 1 ] + a[ 2 ] +……+a[ i ]；（维护一个前缀和）

fmaxn [ i ][ j ]表示从第 i 堆石子合并到第 j 堆石子的最大得分；

fminx [ i ][ j ]表示从第 i 堆石子合并到第 j 堆石子的最小得分；

状态转移方程就是：

fmaxn [ i ][ j ] = max（fmaxn [ i ][ k ] + fmaxn [ k+1 ][ j ]，fmaxn [ i ][ j ]）+ sum [ j ] - sum [ i - 1 ]；

fminx [ i ][ j ] = max（fminx [ i ][ k ] + fminx [ k+1 ][ j ]，fminx [ i ][ j ]）+ sum [ j ] - sum [ i - 1 ]； 

初始条件：fmaxn [ i ][ i ] = 0，fminx [ i ][ i ] = INF；

时间复杂度：O（n³）。

环的处理

题目中石子围成了一个圈，而不是一条线，那么我们怎么处理呢？

方法一：由于石子堆围成一圈，因此我们可以枚举分开的位置，首先将这个圈转化为链，因此要做n次，时间复杂度为：O（n⁴）；

方法二：我们可以将这条链延长两倍，扩展成2n-1堆，其中第1堆与第 n+1 堆完全相同，第 i 堆和第 n+i 堆完全相同，这样我们只要对这2n堆动态规划以后，枚举f [ 1 ][ n ]，f [ 2 ][ n+1 ]……f [ n ][ 2n- 1 ]取最优值即可。时间复杂度为：O（8n³）。

代码如下：

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
int read()
{
    char ch=getchar();
    int a=,x=;
    while(ch<''||ch>'')
    {
        if(ch=='-') x=-x;
        ch=getchar();
    }
    while(ch>=''&&ch<='')
    {
        a=(a<<)+(a<<)+(ch-'');
        ch=getchar();
    }
    return a*x;
}
int n,a[],fminx[][],fmaxn[][];
//a数组是每堆石子的重量;
//fminx[i][j]是将第i堆石子合并到第j堆石子的最小得分
//fmaxn[i][j]是将第i堆石子合并到第j堆石子的最大得分
long long sum[];   //前缀和,第1堆石子到第i堆石子的重量和
int main()
{
    n=read();                      //n堆石子
    for(int i=;i<=n;i++)
    {
        a[i]=read();               //石子重量
        a[n+i]=a[i];               //将链延长两倍
    }
    for(int i=;i<=n*;i++)        //注意这里就是2n了
    {
        sum[i]=sum[i-]+a[i];      //预处理前缀和
        fminx[i][i]=;             //边界条件
        fmaxn[i][i]=;
    }
    for(int i=;i<=n;i++)          //枚举区间长度,以合并的堆数作为阶段
    {
        for(int j=;i<=*n-j+;j++)//枚举区间左端点
        {
            int r=i+j-;           //区间右端点
            fmaxn[j][r]=;         //初始化
            fminx[j][r]=1e9;
            for(int k=j;k<r;k++)   //枚举中间断点
            {
                fmaxn[j][r]=max(fmaxn[j][k]+fmaxn[k+][r],fmaxn[j][r]);   //状态转移方程
                fminx[j][r]=min(fminx[j][k]+fminx[k+][r],fminx[j][r]);
            }
            fmaxn[j][r]+=sum[r]-sum[j-];   //加上第j堆石子到第r堆石子的重量和,利用的就是前缀和
            fminx[j][r]+=sum[r]-sum[j-];
        }
    }
    int minx=1e9,maxn=-1e9;
    for(int i=;i<=n;i++)
    {
        minx=min(minx,fminx[i][i-+n]); //找最后答案
        maxn=max(maxn,fmaxn[i][i-+n]);
    }
    printf("%d\n%d",minx,maxn);    //输出
    return ;
} 

P1063 能量项链

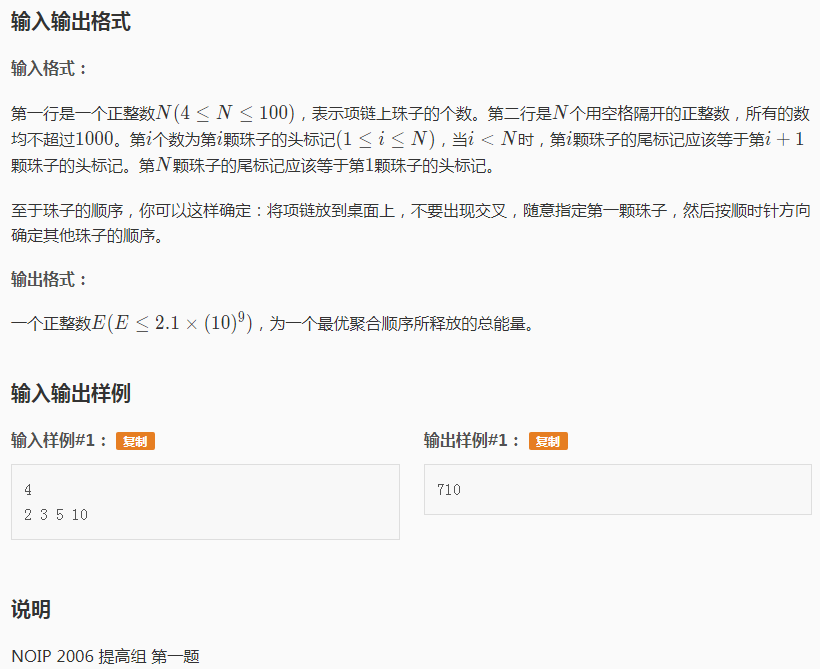
很多同学误把此题理解成确定第一颗珠子后，必须按顺序合并所有的珠子，用贪心的策略，逐一枚举所有珠子为第一颗，选择总能量最大的方案数输出。恰好样例也符合这种逻辑，导致很多同学只得了30分。其实这道题并未要求按顺序合并，事实说明按顺时针方向摆放珠子，合并是可以选择任意相邻两个珠子合并，只要总能量最大即可。

我们用head [ i ]表示第 i 颗珠子的头标记，用 tail [ i ]表示第 i 颗珠子的尾标记，合并两颗相邻珠子所释放的能量为：

Energy=head [ i ] * tail [ i ] * head [ i+1 ]；

合并时不一定按照输入的顺序合并，与石子合并问题类似，可以归结到第n-1次合并，具有明显的动态规划性质。设f [ i ][ j ]表示从第 i 颗珠子合并到第 j 颗珠子所释放的最大能量。假设最后合并的位置 k 和 k+1，则有：

f [ i ][ j ] = max（f [ i ][ k ] + f [ k+1 ][ j ] + head [ i ] * tail [ k ] * head [ j ]），i <= k < j <= n；

上式中，f [ i ][ k ]表示合并第 i 颗珠子到第 k 颗珠子产生的最大能量，f [ k+1 ][ j ]表示合并第 k+1 颗珠子到第 j 颗珠子产生的最大能量，head [ i ] * tail [ k ] * tail [ j ]表示最后一次合并产生的能量。

初始化：f [ i ][ i ] = 0，ans = max{ f [ 1 ][ n ]，f [ 2 ][ n+1 ]，f [ 3 ][ n+2 ]，……，f [ n ][ 2n-1 ] }；

时间复杂度：O（8n³）。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
int read()                              //读入优化
{
    char ch=getchar();
    int a=,x=;
    while(ch<''||ch>'')
    {
        if(ch=='-') x=-x;
        ch=getchar();
    }
    while(ch>=''&&ch<='')
    {
        a=(a<<)+(a<<)+(ch-'');
        ch=getchar();
    }
    return a*x;
}
int n;
int head[],tail[],f[][];
//head是每个珠子的头标记,tail是每个珠子的尾标记;
//f[i][j]表示合并第i颗珠子到第j颗珠子所产生的最大能量
//这里注意要开两倍大小哦
int main()
{
    n=read();
    for(int i=;i<=n;i++)
    {
        head[i]=read();
        head[n+i]=head[i];                       //延长两倍
    }
    for(int i=;i<=*n-;i++) tail[i]=head[i+]; //前一个的尾标记就是后一个的头标记
    tail[*n]=head[];                           //最后一个的尾标记就是第一个的头标记
    for(int i=;i<=n*-;i++) f[i][i]=;         //初始化
    for(int i=;i<=n-;i++)                      //枚举合并次数
    {
        for(int j=;i+j<=n*;j++)                //枚举合并的区间长度
        {
            int r=i+j;                           //区间右端点
            for(int k=j;k<r;k++)                 //枚举中间断点
            f[j][r]=max(f[j][r],f[j][k]+f[k+][r]+head[j]*tail[k]*tail[r]);   //状态转移方程
        }
    }
    int ans=;
    for(int i=;i<=n;i++)
    {
        ans=max(ans,f[i][i-+n]);                //以每个珠子为第一颗珠子,找最大能量
    }
    printf("%d",ans);
    return ;
}

就整理到这里吧~如果有不对的地方请在下方评论哦QwQ~