[CSP-S模拟测试]:二叉搜索树（DP+贪心）

题目传送门（内部题99）

---

输入格式

　　第一行一个整数$n$，第二行$n$个整数$x_1\sim x_n$。

---

输出格式

　　一行一个整数表示答案。

---

样例

样例输入：

5
8 2 1 4 3

样例输出：

35

---

数据范围与提示

样例解释：

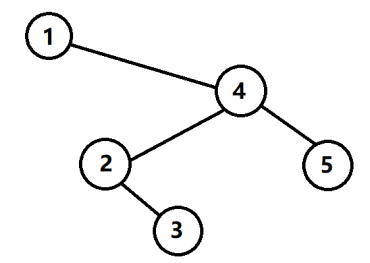
数据范围：

　　对于$10\%$的数据，$n\leqslant 10$。
　　对于$40\%$的数据，$n\leqslant 300$。
　　对于$70\%$的数据，$n\leqslant 2,000$。
　　对于$100\%$的数据，$n\leqslant 5,000,1\leqslant x_i\leqslant 10^9$。

提示：

　　二叉搜索树或者是一棵空树，或者是具有下列性质的二叉树：若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；它的左、右子树也分别为二叉搜索树。

---

题解

因为满足二叉搜索树的性质，所以一棵子树里的点一定是连续的。

考虑$DP$，不妨一步一步来考虑，设$dp[x][l][r]$表示区间$[l,r]$的跟节点深度为$x$的最小代价。

转移很简单，无非就是枚举$[l,r]$中哪个点做跟节点即可，时间复杂度是$\Theta(n^4)$的。

（考虑一个小优化：因为深度其实远远达不到$n$，也就是$\log n$多一点，所以直接扫到$10$左右就能拿到$40$分啦～）

考虑优化，发现深度每增加$1$，也就相当于又加了一个$\sum \limits_{i=l}^r x_i$，用前缀和优化就有了$\Theta(n^3)$的做法了。

接着优化，考虑贪心，因为决策点一定是单调的，做个解释，假设现在要处理区间$[l,r]$，在处理它之前我们已经处理出来了$[l,r-1]$和$[l+1,r]$，并且知道了它们的最优决策点，那么$[l,r]$的最优决策点一定在$[l,r-1]$和$[l+1,r]$的最优决策点之间。

时间复杂度：$\Theta(n^2)$（均摊）。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
int n;
long long v[5001],s[5001];
pair<long long,int> dp[5001][5001];
int main()
{
	memset(dp,0x3f,sizeof(dp));
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		scanf("%lld",&v[i]);
		s[i]=s[i-1]+v[i];
		dp[i][i]=make_pair(v[i],i);
	}
	for(int i=2;i<=n;i++)
	{
		for(int l=1;l<=n-i+1;l++)
		{
			int r=l+i-1;
			for(int mid=dp[l][r-1].second;mid<=dp[l+1][r].second;mid++)
			{
				long long res=s[r]-s[l-1];
				if(l<=mid-1)res+=dp[l][mid-1].first;
				if(mid+1<=r)res+=dp[mid+1][r].first;
				if(res<dp[l][r].first)dp[l][r]=make_pair(res,mid);
			}
		}
	}
	printf("%lld",dp[1][n]);
	return 0;
}

---

rp++