P5657 格雷码【民间数据】

P5657 格雷码【民间数据】

题解

其实这题水啊

打表找规律

【1】0   1

【2】00   01  11  10

【3】000   001   011   010   110   111   101   100

【4】0000   0001   0011   0010   0110   0111   0101   0100

1100   1101   1111    1110   1010   1011   1001   1000

然后我们发现这题其实可以二分做

1.0 真的以为这题很水

n位的二进制格雷码一共有2ⁿ种

目的输出编号为k的二进制格雷码

二分查找，查找区间为[ 0 , 2ⁿ-1 ]

然后我们像剥洋葱一样，从外到内一层一层输出，一共输出n层

（1）如果k在区间左边，那么显然当前最外层的数字应该是0，否则就是1

（2）然后我们继续往下找，继续缩小查找区间

大体框架是酱紫

while(l!=r)
{
    mid=(l+r)>>;
    if(k<=mid) printf("");
    else printf("");
}

2.0  不好好分析题意

其实仔细分析过打表的人会发现，这么做，问题hin大，样例1可以水过，样例2,3就完蛋

问题出在这一句：

我们分析，如果上一层你是从上层区间右边转移到下一层的，那么读题目：

显然是要标记一下，也就是本来应该输出1，实际上你是由上一层逆序得到，所以相应的应该改为输出0

也就是二分思路改为：

（1）若k在当前查找区间左边，如果它是由上一个查找区间的左区间转移过来，输出0，如果它是由上一个查找区间的右区间转移过来，输出1

（2）若k在当前查找区间右边，如果它是由上一个查找区间的左区间转移过来，输出1，如果它是由上一个查找区间的右区间转移过来，输出0

注意：

这里我们用flag标记是否从上一层的右区间转移来

大体框架：

while(l!=r)
    {
        mid=(l+r)>>;
        if(k<=mid){
            if(flag) printf("");
            else printf("");
            r=mid,flag=;
        }
        else{
            if(flag) printf("");
            else printf("");
            l=mid+,flag=;
        }
    }

恭喜你！

我还是第一次看见这样的结果。。。

3.0  暂时性迷惑行为

所以问题出在哪里？？？

和神仙讨论之后呢，发现问题很大啊QAQ

1.要用 unsigned long long ，你看这样就很危险会出现负数（数字超范围）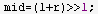   

2.为什么要用while呢（TLE警告）

反正每次都是缩小一半的搜索区间，记录下来这几个数字不就好了

4.0终极版

然后第二天重新整理了下思路，重构代码：

1.由于每次二分查找实际用到的只是区间中点mid，所以我们只把mid移动就好了

注意格雷码编号0~2ⁿ-1，所以mid做了减1处理

2.用for循环实现

3.p定位区间长度，也就是每次搜下一个区间时，mid的移动量

4.flag表示是否由上一个区间的右半边转移来

代码

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<string>
#include<cstring>
#include<queue>

using namespace std;

typedef unsigned long long ll;

inline ll read()
{
    ll ans=;
    char last=' ',ch=getchar();
    while(ch<''||ch>'') last=ch,ch=getchar();
    while(ch>=''&&ch<='') ans=ans*+ch-'',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

ll n,k;
ll num[]={,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,};
bool flag=;

int main()
{
    n=read();k=read();
    ll mid=num[n-]-,p=n-;
    for(int i=;i<=n;i++){
        p--;
        if(k<=mid){
            if(flag) printf("");
            else printf("");
            flag=;
            mid-=num[p];
        }else{
            if(flag) printf("");
            else printf("");
            flag=;
            mid+=num[p];
        }
    }

    return ;
}