[线性代数] 矩阵代数進階：矩阵分解 Matrix factorization

Matrix factorization

导语：承载上集的矩阵代数入门，今天来聊聊进阶版，矩阵分解。其他集数可在[线性代数]标籤文章找到。有空再弄目录什麽的。

Matrix factorization is quite like an application of invertible matrices, where L is an invertible matrix in LU factorization.

As you may have seen, that solving Ax=b for x can be tedious with all the row-reduction algorithm. Here, we are going to explore another efficient algorithm for find x in matrix equation, which is LU Factorization. Suppose we are given L and U in the following form which reconstruct A. L is an invertible unit lower triangular mxm matrix, while U is the mxn echelon form of A. Recall a way to solve for x is by x=A^-1b and A^-1 need to be invertible. Since L is invertible, LU is also invertible as proved in previous article in this series. The motivation here is that if we are to compute x for different b, we need to compute A^-1b_i for every single b. That's not desirable and we should look for ways to circumvent this…

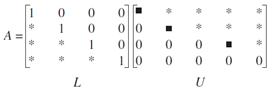
Suppose LU are already given, expressing A=LU is just the first step in LU factorization. Remember our goal of using matrix factorization is to solve for x in matrix equation. So we rely on the following:

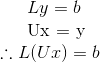
Above suggests by row-reducing the following, we can get x. So we introduce y as the intermediate results along our way to get b. Noted that we still need to calculate each b individually for Ax=b, just that with the assistance of LU, less steps are involved.

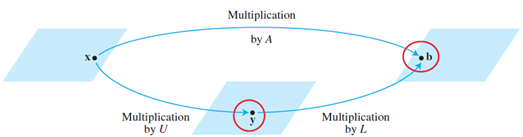
As we know L as an lower unit triangular matrix, columns must be linearly independent. Since it's mxm, L is also invertible. This means the following:

Indeed, when you get a lower triangular unit matrix L, it's trivial to get I_mxm from it. As U is the echelon form of A and is of size mxn, so identity matrix is not guaranteed as the reduced echelon form may not be of square matrix.

The LU factorization algorithm

The prerequisite for using this algorithm is that, given any matrix A in Ax=b, A must be reduceable to echelon form, U, using row replacements of rows in a TOP-DOWN manner. However, this is always a hard requirement to meet and people sometimes relax this restriction into allowing row interchanges before performing top-down sequential row replacement in A. If the requirements are satisfied, it's guaranteed we can get the lower triangular unit matrix L, and the proof of which is shown below:

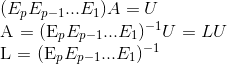
And if we apply the same sequence of elementary matrices onto L, we restore the identity matrix I as follows:

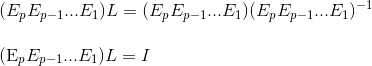
But now it sounds a bit abstract. What exactly does give us btw? And how is it utilized to find L? The following example shows how. During the row-reduction of A into U, entries below pivot position in each pivot column is zeroed-out. The reverse of elementary row operations just require us to gather all pivot columns before their transformation and pack them into a nxn matrix.

When all pivot columns before row replacement gathered, L is easily available.

Examples

例子不定期更新