MIP求解方法总结

*本文主要记录和分享学习到的知识，算不上原创

*参考文献见链接

本文主要简述了求解MIP问题的两大类（精确求解和近似求解），或者更细致地，三大类方法（精确算法，ε-近似算法和启发式算法）。由于暂时不太熟悉ε-近似算法，所以在这个版块我大部分只会涉及到精确算法和启发式算法。

目录

　　MIP问题

　　MIP求解方法

MIP问题

MIP问题，即混合整数规划问题(Mixed integer programming)。

首先我们来简单回顾一下线性规划问题。

线性规划问题

线性规划问题指的是满足：

（1）目标函数是线性函数；

（2）约束条件是线性等式或不等式；

的优化问题。通常是求最小化目标函数或最大化目标函数。

我以下提到的线性规划问题，如果没有特殊说明，指的是最小化目标函数。注意：最小化目标函数与最大化目标函数可以相互转换，没有实质上的区别。

线性规划问题

　　→整数规划问题

　　　　→0-1 问题

　　→混合整数规划问题

线性规划问题，根据对变量的限制，可以更细地区分出：
（1）整数规划问题：指的是变量是整数的线性规划问题。

它将连续的线性规划跳转到离散的整数规划。需要说明的是求解整数规划的难度比求解线性规划的难度要大很多，尤其是当问题的规模很大时。

（2）0-1规划问题：指的是变量只能取值0或1的线性规划问题。

它是整数规划中特殊的一种。

（3）混合整数规划问题：指的是所有变量中有些变量可以取值连续，有些变量只能取整数值的线性规划问题。

混合整数规划问题

根据混合整数规划问题（MIP）的定义，可以概括出其一般形式：

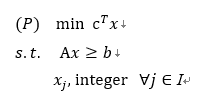
MIP求解方法

MIP的求解方法可以分为：精确求解和近似求解两大类，如下图：

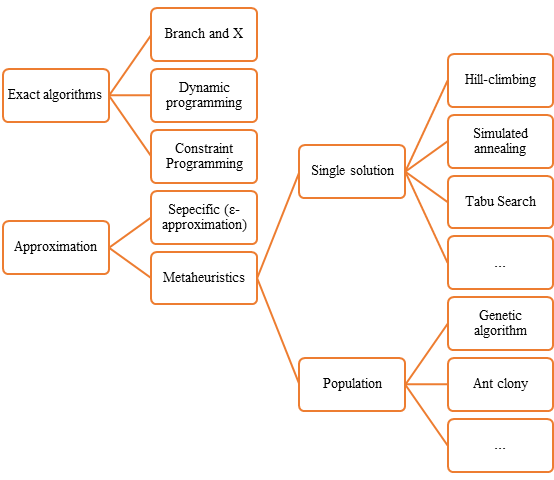
我们简单谈一谈精确求解和近似求解的区别：

（1）精确求解的目标是求得最优解(global optimal solution)，但作为代价求解的过程需要花很长时间(exponential time)，所以更适合于规模比较小的MIP问题。

（2）近似求解并不要求求得最优解，而是希望能在短时间内求得较优解(suboptimal solution)。

近似求解，实际上可以理解成用时间换质量的一种求解思想。

近似求解又可以分为两种大类：

（1）ε-approximation：ε-近似算法要求在短时间内(in polynomial time)求得次优解(suboptimal solution)，并且可以保证解的优秀程度(bound on the degree of suboptimality)。

对于最小化问题而言，一个ε-近似算法在多项式时间内得到的解Z_H满足：

Z_H≤(1+ε)Z^*

其中，Z^*表示该问题的最优解。

（2）metaheuristics：启发式算法往往能在短时间内(empirically fast)获得较优解(suboptimal solution)，但不能保证解的优秀程度(without a gurantee of its quality)。由于启发式算法通常求解速度快，适用于规模中等或规模大的MIP问题，所以企业中常常使用启发式算法求解问题。

*精确算法和启发式算法并不是完全分割的，比如Cplex利用branch and cut思想求解整数规划时，可以调用HeuristicCallback，而variable neighborhood search、local braching等启发式算法在求解大规模问题时可以调用Cplex求解局部最优解。