Adam和学习率衰减（learning learning decay）

梯度下降法更新参数
Adam 更新参数
Adam + 学习率衰减
- Adam 衰减的学习率
References

本文先介绍一般的梯度下降法是如何更新参数的，然后介绍 Adam 如何更新参数，以及 Adam 如何和学习率衰减结合。

梯度下降法更新参数

梯度下降法参数更新公式：
\[
\theta_{t+1} = \theta_{t} - \eta \cdot \nabla J(\theta_t)
\]

其中，$\eta$ 是学习率，$\theta_t$ 是第 $t$ 轮的参数，$J(\theta_t)$ 是损失函数，$\nabla J(\theta_t)$ 是梯度。

在最简单的梯度下降法中，学习率 $\eta$ 是常数，是一个需要实现设定好的超参数，在每轮参数更新中都不变，在一轮更新中各个参数的学习率也都一样。

为了表示简便，令 $g_t = \nabla J(\theta_t)$，所以梯度下降法可以表示为：
\[
\theta_{t+1} = \theta_{t} - \eta \cdot g_t
\]

Adam 更新参数

Adam，全称 Adaptive Moment Estimation，是一种优化器，是梯度下降法的变种，用来更新神经网络的权重。

Adam 更新公式：
\[
\begin{aligned}
m_{t} &=\beta_{1} m_{t-1}+\left(1-\beta_{1}\right) g_{t} \\
v_{t} &=\beta_{2} v_{t-1}+\left(1-\beta_{2}\right) g_{t}^{2} \\
\hat{m}_{t} &=\frac{m_{t}}{1-\beta_{1}^{t}} \\
\hat{v}_{t} &=\frac{v_{t}}{1-\beta_{2}^{t}} \\
\theta_{t+1}&=\theta_{t}-\frac{\eta}{\sqrt{\hat{v}_{t}}+\epsilon} \hat{m}_{t}
\end{aligned}
\]

在 Adam 原论文以及一些深度学习框架中，默认值为 $\eta = 0.001$，$\beta_1 = 0.9$，$\beta_2 = 0.999$，$\epsilon = 1e-8$。其中，$\beta_1$ 和 $\beta_2$ 都是接近 1 的数，$\epsilon$ 是为了防止除以 0。$g_{t}$ 表示梯度。

咋一看很复杂，接下一一分解：

前两行：
\[
\begin{aligned}
m_{t} &=\beta_{1} m_{t-1}+\left(1-\beta_{1}\right) g_{t} \\
v_{t} &=\beta_{2} v_{t-1}+\left(1-\beta_{2}\right) g_{t}^{2}
\end{aligned}
\]

这是对梯度和梯度的平方进行滑动平均，即使得每次的更新都和历史值相关。

中间两行：
\[
\begin{aligned}
\hat{m}_{t} &=\frac{m_{t}}{1-\beta_{1}^{t}} \\
\hat{v}_{t} &=\frac{v_{t}}{1-\beta_{2}^{t}}
\end{aligned}
\]
这是对初期滑动平均偏差较大的一个修正，叫做 bias correction，当 $t$ 越来越大时，$1-\beta_{1}^{t}$ 和 $1-\beta_{2}^{t}$ 都趋近于 1，这时 bias correction 的任务也就完成了。
最后一行：
\[
\theta_{t+1}=\theta_{t}-\frac{\eta}{\sqrt{\hat{v}_{t}}+\epsilon} \hat{m}_{t}
\]

这是参数更新公式。

学习率为 $\frac{\eta}{\sqrt{\hat{v}_{t}}+\epsilon}$，每轮的学习率不再保持不变，在一轮中，每个参数的学习率也不一样了，这是因为 $\eta$ 除以了每个参数 $\frac{1}{1- \beta_2} = 1000$ 轮梯度均方和的平方根，即 $\sqrt{\frac{1}{1000}\sum_{k = t-999}^{t}g_k^2}$。而每个参数的梯度都是不同的，所以每个参数的学习率即使在同一轮也就不一样了。（可能会有疑问，$t$ 前面没有 999 轮更新怎么办，那就有多少轮就算多少轮，这个时候还有 bias correction 在。）

而参数更新的方向也不只是当前轮的梯度 $g_t$ 了，而是当前轮和过去共 $\frac{1}{1- \beta_1} = 10$ 轮梯度的平均。

有关滑动平均的理解，可以参考我之前的博客：理解滑动平均(exponential moving average)。

Adam + 学习率衰减

在 StackOverflow 上有一个问题 Should we do learning rate decay for adam optimizer - Stack Overflow，我也想过这个问题，对 Adam 这些自适应学习率的方法，还应不应该进行 learning rate decay？

我简单的做了个实验，在 cifar-10 数据集上训练 LeNet-5 模型，一个采用学习率衰减 tf.keras.callbacks.ReduceLROnPlateau(patience=5)，另一个不用。optimizer 为 Adam 并使用默认的参数，$\eta = 0.001$。结果如下：

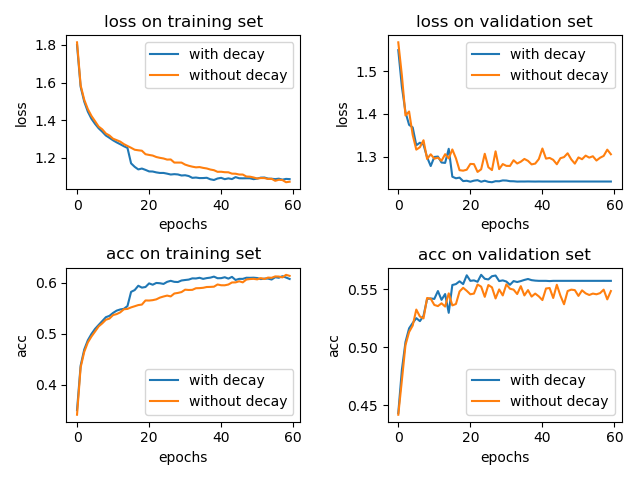
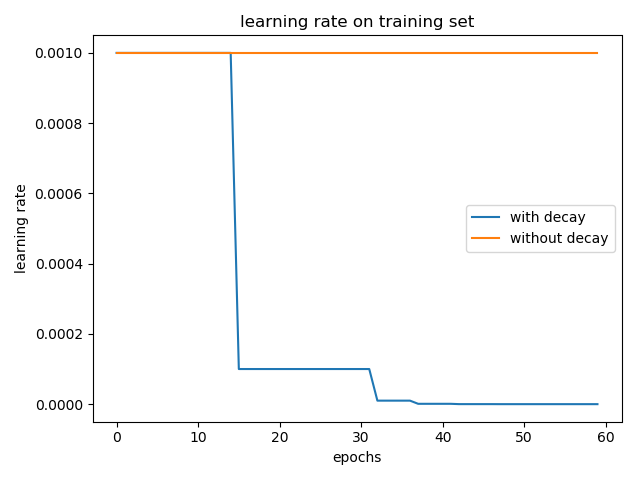
加入学习率衰减和不加两种情况在 test 集合上的 accuracy 分别为: 0.5617 和 0.5476。（实验结果取了两次的平均，实验结果的偶然性还是有的）

通过上面的小实验，我们可以知道，学习率衰减还是有用的。（当然，这里的小实验仅能代表一小部分情况，想要说明学习率衰减百分之百有效果，得有理论上的证明。）

当然，在设置超参数时就可以调低 $\eta$ 的值，使得不用学习率衰减也可以达到不错的效果。

将学习率从默认的 0.001 改成 0.0001，epoch 增大到 120，实验结果如下所示：

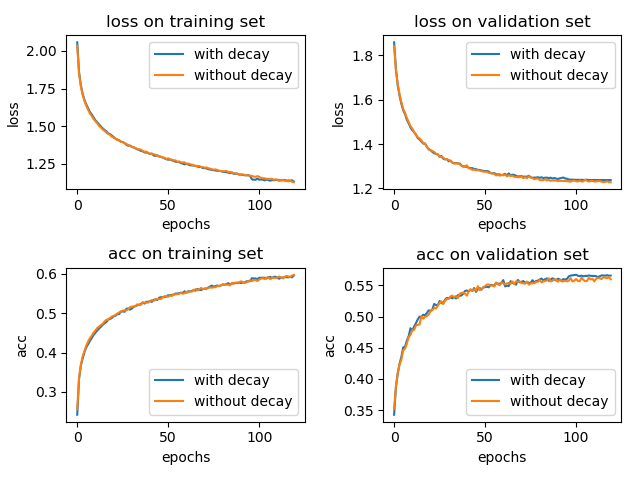
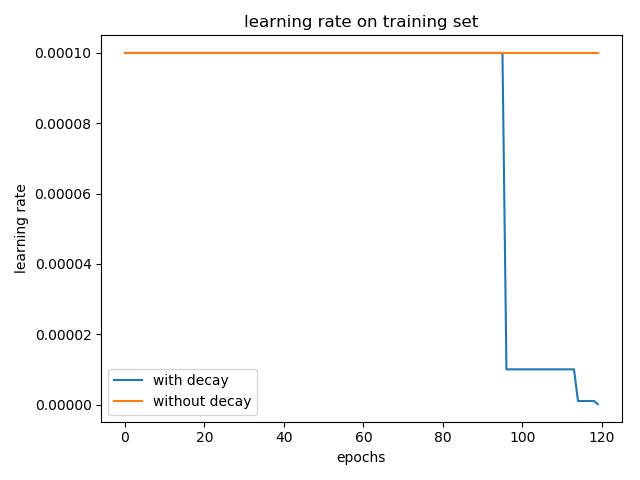
加入学习率衰减和不加两种情况在 test 集合上的 accuracy 分别为: 0.5636 和 0.5688。（三次实验平均，实验结果仍具有偶然性）

这个时候，使用学习率衰减带来的影响可能很小。

那么问题来了，Adam 做不做学习率衰减呢？
我个人会选择做学习率衰减。（仅供参考吧。）在初始学习率设置较大的时候，做学习率衰减比不做要好；而当初始学习率设置就比较小的时候，做学习率衰减似乎有点多余，但从 val set 上的效果看，做了学习率衰减还是可以有丁点提升的。

ReduceLROnPlateau 在 val_loss 正常下降的时候，对学习率是没有影响的，只有在 patience（默认为 10）个 epoch 内，val_loss 都不下降 1e-4 或者直接上升了，这个时候降低学习率确实是可以很明显提升模型训练效果的，在 val_acc 曲线上看到一个快速上升的过程。对于其它类型的学习率衰减，这里没有过多地介绍。

Adam 衰减的学习率

从上述学习率曲线来看，Adam 做学习率衰减，是对 $\eta$ 进行，而不是对 $\frac{\eta}{\sqrt{\hat{v}_{t}}+\epsilon}$ 进行，但有区别吗？

学习率衰减一般如下：

exponential_decay：
decayed_learning_rate = learning_rate * decay_rate ^ (global_step / decay_steps)
natural_exp_decay：
decayed_learning_rate = learning_rate * exp(-decay_rate * global_step / decay_steps)
ReduceLROnPlateau
如果被监控的值（如‘val_loss’）在 patience 个 epoch 内都没有下降，那么学习率衰减，乘以一个 factor
decayed_learning_rate = learning_rate * factor

这些学习率衰减都是直接在原学习率上乘以一个 factor ，对 $\eta$ 或对 $\frac{\eta}{\sqrt{\hat{v}_{t}}+\epsilon}$ 操作，结果都是一样的。

References

An overview of gradient descent optimization algorithms -- Sebastian Ruder
Should we do learning rate decay for adam optimizer - Stack Overflow
Tensorflow中learning rate decay的奇技淫巧 -- Elevanth