hdoj--3594--Cactus（tarjan）

Cactus

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)

Total Submission(s): 1580    Accepted Submission(s): 730

Problem Description

1. It is a Strongly Connected graph.

2. Each edge of the graph belongs to a circle and only belongs to one circle.

We call this graph as CACTUS.








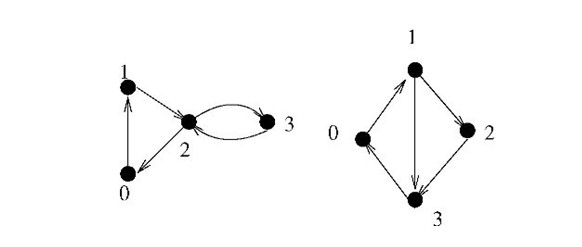
There is an example as the figure above. The left one is a cactus, but the right one isn’t. Because the edge (0, 1) in the right graph belongs to two circles as (0, 1, 3) and (0, 1, 2, 3).

 

Input

The input consists of several test cases. The first line contains an integer T (1<=T<=10), representing the number of test cases.

For each case, the first line contains a integer n (1<=n<=20000), representing the number of points.

The following lines, each line has two numbers a and b, representing a single-way edge (a->b). Each case ends with (0 0).

Notice: The total number of edges does not exceed 50000.

 

Output

For each case, output a line contains “YES” or “NO”, representing whether this graph is a cactus or not.

 

Sample Input

2
4
0 1
1 2
2 0
2 3
3 2
0 0
4
0 1
1 2
2 3
3 0
1 3
0 0

 

Sample Output

YES
NO
#include<stdio.h>
#include<string.h>
#include<queue>
#include<stack>
#include<vector>
#include<algorithm>
using namespace std;
#define M 100000+20
int low[M],dfn[M];
bool Instack[M];
int sccno[M],head[M];
int scc_cnt,cnt,dfs_clock;
int n,flog;
stack<int>s;
vector<int>G[M];
vector<int>scc[M];
struct node
{
	int u,v;
	int next;
}edge[M*2];
void init()
{
	memset(head,-1,sizeof(head));
	cnt=0;
	flog=0;
}
void add(int u,int v)
{
	edge[cnt].u=u;
	edge[cnt].v=v;
	edge[cnt].next=head[u];
	head[u]=cnt++;
}
void getmap()
{
	int a,b;
	scanf("%d",&n);
	while(scanf("%d%d",&a,&b),a||b)
	{
		add(a,b);
	}
}
void tarjan(int u,int fa)
{
	int v;
	low[u]=dfn[u]=++dfs_clock;
	Instack[u]=true;
	s.push(u);
	for(int i=head[u];i!=-1;i=edge[i].next)
	{
		v=edge[i].v;
		if(!dfn[v])
		{
			tarjan(v,u);
			low[u]=min(low[u],low[v]);
		}
		else if(Instack[v])
		{
			low[u]=min(low[u],dfn[v]);
			if(low[v]!=dfn[v])
			flog=1;
		}
	}
	if(low[u]==dfn[u])
	{
		scc_cnt++;
		for(;;)
		{
			v=s.top();
			s.pop();
			Instack[v]=false;
			scc[scc_cnt].push_back(v);
			if(v==u) break;
		}
	}
}
void find(int l,int r)
{
	memset(low,0,sizeof(low));
	memset(dfn,0,sizeof(dfn));
	memset(Instack,false,sizeof(Instack));
	memset(sccno,0,sizeof(sccno));
	scc_cnt=dfs_clock=0;
	for(int i=0;i<n-1;i++)
	{
		if(!dfn[i])
		tarjan(i,-1);
	}
}
void slove()
{
	if(scc_cnt==1&&flog==0)
	printf("YES\n");
	else
	printf("NO\n");
}
int main()
{
	int t;
	scanf("%d",&t);
	while(t--)
	{
		init();
		getmap();
		find(0,n-1);
		slove();
	}
}