Fiborial 题解——2019.10.14

一看到这个题

就感觉。。。cao,,

什么东西。。。？？！

然后就开始暴力求Fn

然鹅我并不会写高精（我太菜了）

只能求到大概10左右

在吧Fn给质因数分解

求出其因子个数

妄图找到什么有关的规律

但是我太过于弱小

并未找到。。。。。。。

（yjg:你找不到规律，并不代表没有规律）

然而我还瞎jb乱模

导致局面甚是混乱

但是，，，，

质因数分解貌似有点苗头，，，

而且这个东西

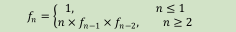
像极了斐波那契数列

那如果是两相结合

就是正解！！！

我的40分代码：

可能是写的太过繁琐

导致TLE

#include<cstdio>
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
const int mod=1e9+;
int f[][];
int n;
int main() {
    freopen("fiborial.in","r",stdin);
    freopen("fiborial.out","w",stdout);
    cin>>n;
    for(int i=; i<=n; i++) {
        int k=i,t=;
        for(int j=; j<=i; j++)
            f[][j]=f[][j]+f[][j],f[][j]%=mod;
        while(k>) {
            while(k%t==) {
                k/=t;
                f[][t]++;
            }
            t++;
        }
        for(int j=; j<=i; j++) {
            f[][j]=f[][j];
            f[][j]=f[][j];
        }
    }
    long long ans=;
    for(int i=; i<=n; i++)
        ans*=(f[][i]+),ans%=mod;
    cout<<ans;

    fclose stdin;
    fclose stdout;
    return ;
}

那么就让我们看看

牛逼哄哄的土蛋的代码吧

上！

#include <cstdio>
#include <cstdlib>

typedef long long ll;

const int N = (int)5e6;
const int S = (int)1e6;

const int mod = (int)1e9 + ;
int f[N + ], n, p[S + ], cnt = , m[N + ], c[N + ];
bool v[N + ];

inline int add(int a, int b) {
    int r = a + b;
    return r >= mod ? r - mod : r;
}

int main() {
    freopen("fiborial.in", "r", stdin);
    freopen("fiborial.out", "w", stdout);

    scanf("%d", &n);
    f[] = f[] = ;
    for (int i = ; i <= n; ++i) f[i] = add(f[i - ], f[i - ]);
    for (int i = ; i <= n; ++i) {
        if (!v[i]) p[cnt++] = i, m[i] = i;
        for (int j = , tmp; j < cnt && (tmp = i * p[j]) <= n; ++j) {
            v[tmp] = true, m[tmp] = p[j];
            if (!(i % p[j])) break;
        }
    }

    for (int i = ; i <= n; ++i)
        for (int x = i; x != ; x /= m[x])
            c[m[x]] = add(c[m[x]], f[n - i]);
    int ans = ;
    for (int i = ; i < cnt; ++i)
        ans = (ll)ans * (c[p[i]] + ) % mod;
    printf("%d\n", ans);

    return ;
}