Legendre polynomials

In mathematics, Legendre functions are solutions to Legendre's differential equation:

In particular, it occurs when solving Laplace's equation (and relatedpartial differential equations) in spherical coordinates.

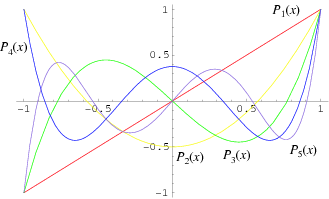
The polynomials may be denoted by P_n(x) , called the Legendre polynomial of order n. The polynomials are either even or odd functions of x for even or odd orders n. The first few polynomials are shown below.

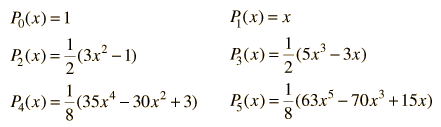
The general form of a Legendre polynomial of order n is given by the sum:

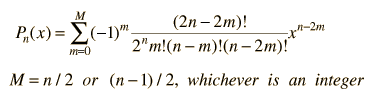
From the Legendre polynomials can be generated another important class of functions for physical problems, the associated Legendre functions.