Conjugate prior relationships

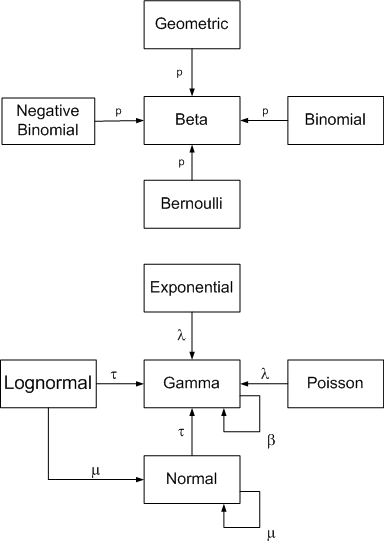
The following diagram summarizes conjugate prior relationships for a number of common sampling distributions.

Arrows point from a sampling distribution to its conjugate prior distribution. The symbol near the arrow indicates which parameter the prior is unknown.

These relationships depends critically on choice of parameterization, some of which are uncommon. This page uses the parameterizations
that make the relationships simplest to state, not necessarily the most common parameterizations. See footnotes below.

Click on a distribution to see its parameterization. Click
on an arrow to see posterior parameters.

See this page for more
diagrams on this site including diagrams for probability and statistics, analysis, topology, and category theory. Also, please contact me if you’re interested in Bayesian
statistical consulting.

Parameterizations

Let C(n, k)
denote the binomial
coefficient(n, k).

The geometric distribution has only one parameter, p,
and has PMF f(x)
= p (1-p)x.

The binomial distribution with parameters n and p has
PMF f(x)
= C(n, x) px(1-p)n-x.

The negative binomial distribution with parameters r and p has
PMF f(x)
= C(r + x –
1, x)pr(1-p)x.

The Bernoulli distribution has probability of success p.

The beta distribution has PDF f(p)
= Γ(α + β) pα-1(1-p)β-1 /
(Γ(α) Γ(β)).

The exponential distribution parameterized in terms of the rate λ has PDF f(x)
= λ exp(-λ x).

The gamma distribution parameterized in terms of the rate has PDF f(x)
= βα xα-1exp(-β x)
/ Γ(α).

The Poisson distribution has one parameter λ and PMF f(x)
= exp(-λ) λx/ x!.

The normal distribution parameterized in terms of precision τ (τ = 1/σ2)

has PDF f(x)
= (τ/2π)1/2 exp( -τ(x –
μ)2/2 ).

The lognormal distribution parameterized in terms of precision τ has PDF f(x)
= (τ/2π)1/2exp( -τ(log(x)
– μ)2/2 ) / x.

Posterior parameters

For each sampling distribution, assume we have data x1, x2,
…, xn.

If the sampling distribution for x is binomial(m, p)
with m known, and the prior distribution is beta(α,
β), the posterior distribution for p is beta(α
+ Σxi,
β + mn – Σxi).
The Bernoulli is the special case of the binomial with m =
1.

If the sampling distribution for x is negative
binomial(r, p) with r known,
and the prior distribution is beta(α, β), the posterior distribution for p is beta(α
+ nr, β + Σxi).
Thegeometric is the special case of the negative binomial with r =
1.

If the sampling distribution for x is gamma(α,
β) with α known, and the prior distribution on β is gamma(α0,
β0), the posterior distribution
for β is gamma(α0 + n,
β0 + Σxi).
Theexponential is a special case of the gamma with α = 1.

If the sampling distribution for x is Poisson(λ),
and the prior distribution on λ is gamma(α0,
β0), the posterior on λ is gamma(α0 +
Σxi, β0 + n).

If the sampling distribution for x is normal(μ, τ) with τ known, and the prior distribution on μ is normal(μ0,
τ0), the posterior distribution
on μ is normal((μ0 τ0 +
τ Σxi)/(τ0 + nτ),
τ0 + nτ).

If the sampling distribution for x is normal(μ, τ) with μ known, and the prior distribution on τ is gamma(α,
β), the posterior distribution on τ is gamma(α + n/2,
(n-1)S2)
where S2 is
the sample variance.

If the sampling distribution for x is lognormal(μ, τ) with τ known, and the prior distribution on μ is normal(μ0,
τ0), the posterior distribution
on μ is normal((μ0 τ0 +
τ Πxi)/(τ0 + nτ),
τ0 +nτ).

If the sampling distribution for x is lognormal(μ,
τ) with μ known, and the prior distribution on τ is gamma(α, β), the posterior distribution on τ is gamma(α
+ n/2, (n-1)S2)
where S2 is
the sample variance.

References

A
compendium of conjugate priors by Daniel Fink.

See also Wikipedia’s article on conjugate
priors.