『Two 树的直径求解及其运用』

<更新提示>

<第一次更新>

<正文>

树的直径

我们先来认识一下树的直径。

树是连通无环图，树上任意两点之间的路径是唯一的。定义树上任意两点$u, v$的距离为$u$到$v$路径上边权的和。树的直径$MN$为树上最长路径，即点$M$和$N$是树上距离最远的两个点，这条路径亦称为树的最长链。

那么，我们考虑一下如何求解树的直径。

方法一：$DP$求解树的直径。

设$d_x$表示从节点$x$出发走向以$x$为根的子树，能够达到的最远距离。

那么

\[d_x=\max_{y\in son(x)}\{d_y+e(x,y)\}
\]

($y$为$x$的一个子节点，$e(x,y)$为从$x$到$y$的权值)

设$f_x$代表经过节点$x$的最长链的长度，则树的直径为$\max_{1 \leq x \leq n}\{f_x\}$。

考虑如何求解$x$。对于$x$的任意两个子节点$y_i$和$y_j$，$f_x$由四部分组成，$y_i$到其子树中的最远距离，$e(y_i,x)$，$e(x,y_j)$，$y_j$到其子树中的最远距离。所以

\[f_x=\max_{y_i,y_j\in son(x)}\{d_{y_i}+d_{y_j}+e(y_i,x)+e(x,y_j)\}
\]

注意到$d_{y_i}+e(y_i,x)$和$d_{y_j}+e(y_j,x)$的格式的相同的，都是用于更新$d_x$的项，我们可以在枚举到一个新的$y$时利用上一个$d_x$的值顺带更$f_x$，即用$d_x+d_{y_i}+e(y_i,x)$，实现$O(n)$求解树的直径。

$Code:$

#include<cstdio>

#include<iostream>

#include<vector>

#include<cstring>

#define mset(name,val) memset(name,val,sizeof name)

using namespace std;

const int N=40000+50;

int n,m,ans,vis[N],d[N],f[N];

struct edge{int val,ver;};

vector < edge > Link[N];

inline void input(void)

{

	scanf("%d%d",&n,&m);

	for(int i=1;i<=m;i++)

	{

		int x,y,v;

		scanf("%d%d%d",&x,&y,&v);

		Link[x].push_back((edge){v,y});

		Link[y].push_back((edge){v,x});

	}

}

inline int dp(int x)

{

	vis[x]=true;

	for(int i=0;i<Link[x].size();i++)

	{

		int y=Link[x][i].ver;

		if(!vis[y])

		{

			dp(y);

			f[x]=max(f[x],d[x]+d[y]+Link[x][i].val);

			d[x]=max(d[x],d[y]+Link[x][i].val);

		}

	}

	ans=max(ans,f[x]);

}

int main(void)

{

	input();

	dp(1);

	printf("%d\n",ans);

	return 0;

}

方法二：两次$BFS/DFS$求解树的直径

①从树上任意一点$P$出发，找到距离它最远的一点$M$

②再从$M$出发，找到距离它最远的一点$N$

③$MN$即为树的直径

时间复杂度$O(n)$。

证明如下：

反证法：假设$M$不是直径的一个端点，$AB$是树的直径。

① 如果$P$是直径上的点，如图，$PM > PB$

则$AP + PM > AP + PB = AB$这与$AB$是直径矛盾。

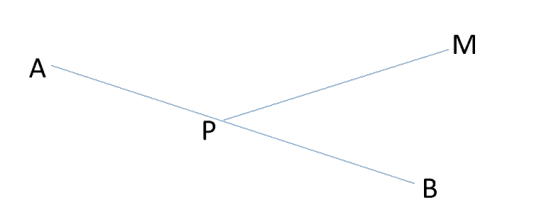
② $P$到$M$路径与$A$到$B$路径有公共结点$T$，如图

$PT + TM > PT + TB$，则$TM > TB$，故$AT + TM > AT + TB = AB$，矛盾。

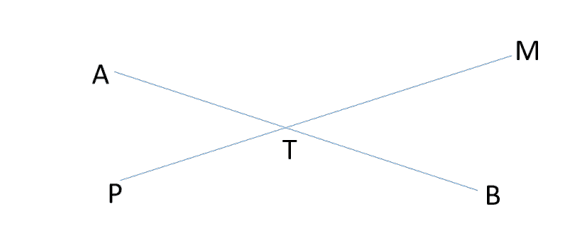
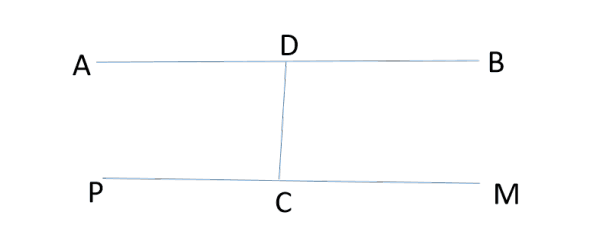
③ $P$到$M$的路径与$A$到$B$的路径无公共结点，如图

$PC + CM > PC + CD + BD$，则$CM > CD + BD，CM + CD > BD$

故$CM + CD + AD > BD + AD = AB$，矛盾。

$Code:$

#include<cstdio>

#include<iostream>

#include<queue>

#include<vector>

#include<cstring>

#define mset(name,val) memset(name,val,sizeof name)

using namespace std;

const int N=40000+50;

int n,m,ans,vis[N],dis[N];

struct edge{int val,ver;};

vector < edge > Link[N];

inline void input(void)

{

	scanf("%d%d",&n,&m);

	for(int i=1;i<=m;i++)

	{

		int x,y,v;

		scanf("%d%d%d",&x,&y,&v);

		Link[x].push_back((edge){v,y});

		Link[y].push_back((edge){v,x});

	}

}

inline int Search(int start)

{

	queue< int >q;

	mset(vis,0x00);

	mset(dis,0x00);

	vis[start]=1;

	q.push(start);

	while(!q.empty())

	{

		int temp=q.front();q.pop();

		for(int i=0;i<Link[temp].size();i++)

		{

			if(!vis[Link[temp][i].ver])

			{

				vis[Link[temp][i].ver]=true;

				dis[Link[temp][i].ver]=dis[temp]+Link[temp][i].val;

				q.push(Link[temp][i].ver);

			}

		}

	}

	int res=0,Maxdis=0;

	for(int i=1;i<=n;i++)

	{

		if(dis[i]>Maxdis)

		{

			Maxdis=dis[i];

			res=i;

		}

	}

	return res;

}

int main(void)

{

	input();

	int p=Search(1);

	printf("%d\n",dis[Search(p)]);

	return 0;

}

我们通过一道例题详细地了解一下。

Two(POJ1849)

Description

The city consists of intersections and streets that connect them.

Heavy snow covered the city so the mayor Milan gave to the winter-service a list of streets that have to be cleaned of snow. These streets are chosen such that the number of streets is as small as possible but still every two intersections to be connected i.e. between every two intersections there will be exactly one path. The winter service consists of two snow plovers and two drivers, Mirko and Slavko, and their starting position is on one of the intersections.

The snow plover burns one liter of fuel per meter (even if it is driving through a street that has already been cleared of snow) and it has to clean all streets from the list in such order so the total fuel spent is minimal. When all the streets are cleared of snow, the snow plovers are parked on the last intersection they visited. Mirko and Slavko don’t have to finish their plowing on the same intersection.

Write a program that calculates the total amount of fuel that the snow plovers will spend.

Input Format

The first line of the input contains two integers: N and S, 1 <= N <= 100000, 1 <= S <= N. N is the total number of intersections; S is ordinal number of the snow plovers starting intersection. Intersections are marked with numbers 1...N.

Each of the next N-1 lines contains three integers: A, B and C, meaning that intersections A and B are directly connected by a street and that street's length is C meters, 1 <= C <= 1000.

Output Format

Write to the output the minimal amount of fuel needed to clean all streets.

Sample Input

Sample Output

解析

题目大意就是有一棵树，在s结点放两个机器人，这两个机器人会把树的每条边都走一遍, 但是最后机器人不要求回到出发点。问你两个机器人走的路总长之和的最小值是多少?

首先，我们假设只有一个机器人，那么答案是什么？

我们可以让机器人沿着从起点开始的某一条最远距离路径走，对于路径上的其他子树，机器人需要进入遍历，并返回，需要花费两倍的子树权值和，但由于机器人不需要回到起点，所以答案为$2*\sum w_i-d$，$d$为出发点所能到达的最远距离。同理，如果有两个机器人，那么我们就让他们分别向两条不同的路径走去，这样就正好对应了树的直径的$BFS/DFS$求法，机器人走的路径就成了树的直径，那么最终的答案就是$2*\sum w_i-D$，$D$为树的直径长度。

$Code:$

#include<cstdio>

#include<iostream>

#include<queue>

#include<vector>

#include<cstring>

#define mset(name,val) memset(name,val,sizeof name)

using namespace std;

const int N=100000+50;

int n,s,sum,vis[N],dis[N];

struct edge{int val,ver;};

vector < edge > Link[N];

inline void input(void)

{

	scanf("%d%d",&n,&s);

	for(int i=1;i<n;i++)

	{

		int x,y,v;

		scanf("%d%d%d",&x,&y,&v);

		Link[x].push_back((edge){v,y});

		Link[y].push_back((edge){v,x});

		sum+=v*2;

	}

}

inline int Search(int start)

{

	queue< int >q;

	mset(vis,0x00);

	mset(dis,0x00);

	vis[start]=1;

	q.push(start);

	while(!q.empty())

	{

		int temp=q.front();q.pop();

		for(int i=0;i<Link[temp].size();i++)

		{

			if(!vis[Link[temp][i].ver])

			{

				vis[Link[temp][i].ver]=true;

				dis[Link[temp][i].ver]=dis[temp]+Link[temp][i].val;

				q.push(Link[temp][i].ver);

			}

		}

	}

	int res=0,Maxdis=0;

	for(int i=1;i<=n;i++)

	{

		if(dis[i]>Maxdis)

		{

			Maxdis=dis[i];

			res=i;

		}

	}

	return res;

}

int main(void)

{

	input();

	int p=Search(s);

	printf("%d\n",sum-dis[Search(p)]);

	return 0;

}

<后记>