Noip模拟33垫底反思 2021.8.8

T1 Hunter

考场上没写$%p$挂了25分。也是很牛皮，以后打完过了样例一定要检查

因为样例太小了。。。。。。很容易忘记%%%%

正解随便手模就出来了。

 1 #include<bits/stdc++.h>
 2 #define int long long
 3 using namespace std;
 4 const int NN=1e5+5,p=998244353;
 5 int n,w[NN],ans;
 6 inline int qmo(int a){
 7     int ans=1,b=p-2,c=p; a%=c;
 8     while(b){ if(b&1) ans=(ans*a)%c; b>>=1; a=(a*a)%c; }return ans;
 9 }
10 namespace WSN{
11     inline short main(){
12         scanf("%lld",&n); for(int i=1;i<=n;i++) scanf("%lld",&w[i]);
13         for(int i=2;i<=n;i++) (ans+=w[i]*qmo((w[1]+w[i])%p)%p)%=p;
14         printf("%lld\n",ans+1);    return 0;
15     }
16 }
17 signed main(){return WSN::main();}

T2 Defence

据说是很水的动态开点权值线段树板子。。。。。

想到用线段数维护的值，但是不会打动态开点了。。。

数据结构太弱了，码力太弱了。。。。。决定以后有时间就打数据结构

恶心死自己的那种。。。盯着代码望穿秋水的那种。。。

基本思路：

维护的信息有第一个一的位置，最后一个一的位置，区间内最长的$0$串的长度

每个点开一颗权值线段树，维护当时使用完法术后的序列信息

然后$dfs$到叶子节点向上做线段树合并，在合并的时候统计节点的信息记录答案就行了。

真是做过的题也不记得了，这不就是玫瑰花精吗？？？？

原来数据结构学习的太不走心了，以后是要背锅的，前面付出的太少了。。。。

代码能力是要一点一点练的，不是想想题看看代码就会的，以后一定要多自己码，唉～

思路是很简单的，考场上还是可以想到的，但是被自己的码力限制了，苦恼

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 const int NN=1e5+5;
 4 int n,m,q,rt[NN],ans[NN];
 5 struct SNOW{int to,next;};SNOW e[NN<<1];int head[NN],rp;
 6 inline void add(int x,int y){e[++rp]=(SNOW){y,head[x]}; head[x]=rp;}
 7 struct SNOWtree{
 8     int seg,ls[NN*40],rs[NN*40];
 9     int pre[NN*40],nxt[NN*40],len[NN*40];
10     inline void pushup(int x){
11         if(!ls[x]){pre[x]=pre[rs[x]]; nxt[x]=nxt[rs[x]]; len[x]=len[rs[x]]; return;}
12         if(!rs[x]){pre[x]=pre[ls[x]]; nxt[x]=nxt[ls[x]]; len[x]=len[ls[x]]; return;}
13         int lenth=pre[rs[x]]-nxt[ls[x]]-1;
14         len[x]=max(lenth,max(len[ls[x]],len[rs[x]]));
15         pre[x]=min(pre[ls[x]],pre[rs[x]]);
16         nxt[x]=max(nxt[ls[x]],nxt[rs[x]]);
17     }
18     inline void insert(int &x,int l,int r,int pos){
19         if(!x) x=++seg;
20         if(l==r){
21             pre[x]=nxt[x]=pos;
22             len[x]=0;
23             return;
24         }int mid=l+r>>1;
25         if(pos<=mid) insert(ls[x],l,mid,pos);
26         else insert(rs[x],mid+1,r,pos);
27         pushup(x);
28     }
29     inline void merge(int &x,int y,int l,int r){
30         if(!x||!y) {x=x+y;return;}
31         if(l==r){
32             if(pre[y]){
33                 pre[x]=nxt[x]=l;
34                 len[x]=0;
35             }
36             return;
37         }int mid=l+r>>1;
38         merge(ls[x],ls[y],l,mid);
39         merge(rs[x],rs[y],mid+1,r);
40         pushup(x);
41     }
42 }tr;
43 inline void dfs(int f,int x){
44     for(int i=head[x];i;i=e[i].next){
45         int y=e[i].to; if(y==f) continue;
46         dfs(x,y);
47         tr.merge(rt[x],rt[y],1,m);
48     }
49     if(!tr.pre[rt[x]]) ans[x]=-1;
50     else ans[x]=max(tr.pre[rt[x]]+m-tr.nxt[rt[x]]-1,tr.len[rt[x]]);
51 }
52 namespace WSN{
53     inline short main(){
54         scanf("%d%d%d",&n,&m,&q);
55         for(int i=1,u,v;i<n;i++){
56             scanf("%d%d",&u,&v);
57             add(u,v); add(v,u);
58         }
59         for(int i=1,u,pos;i<=q;i++){
60             scanf("%d%d",&u,&pos);
61             tr.insert(rt[u],1,m,pos);
62         }dfs(0,1);
63         for(int i=1;i<=n;i++) printf("%d\n",ans[i]);
64         return 0;
65     }
66 }
67 signed main(){return WSN::main();}

T3 Connect

本次考试第二坑点，打了$spj$函数却没有调用。。。。失掉20分。。

两处失误当时只要是挽回一处都不会垫底。。。。

以后考试结束前十分钟一定要抽出时间检查自己提交的代码，不能再出失误了。。

数据范围提示状态压缩$dp$，思路比较神

$1$号点到$N$的路径唯一相当于存在一条$1$到$N$的链, 并且不在链上的每个联通块最多只和链上的一个点有连边

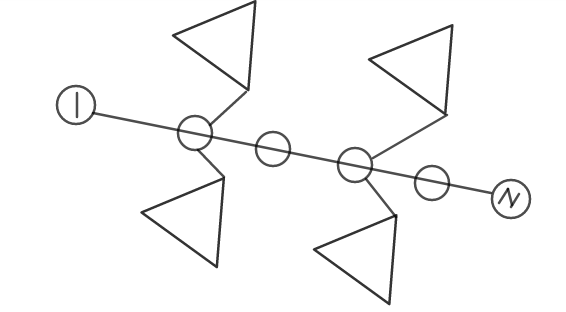
类似这样。那么我们要预处理出来的值就知道了。

$sum[S]$表示状态$S$的联通块中的边权总和

$to[S][i]$表示联通块$S$到$i$点的连边总和

那么$dp_{S,i}$就表示目前的状态为$S$，链的末端点为$i$的边权最大值，最后用总边权减去就可以得到删去边的最小值

看题解是完全能看明白的，粘一张图片

 1 #include<bits/stdc++.h>
 2 #define int long long
 3 using namespace std;
 4 const int NN=17;
 5 int n,m,g[NN][NN],U,dp[1<<NN][NN],sum[1<<NN],to[1<<NN][NN];
 6 inline void pre(){
 7     for(int S=1;S<=U;S++) for(int i=0;i<n;i++) for(int j=i+1;j<n;j++)
 8         if((S>>i&1)&&(S>>j&1)) sum[S]+=g[i][j];
 9     for(int S=1;S<=U;S++) for(int i=0;i<n;i++) for(int j=0;j<n;j++)
10         if((S>>j&1)&&g[i][j]) to[S][i]+=g[i][j];
11 }
12 namespace WSN{
13     inline short main(){
14         scanf("%lld%lld",&n,&m); U=(1<<n)-1;
15         for(int i=1,u,v,w;i<=m;i++){
16             scanf("%lld%lld%lld",&u,&v,&w);--u;--v;
17             g[u][v]=g[v][u]=w;
18         }
19         pre(); memset(dp,-1,sizeof(dp));
20         dp[1][0]=0;
21         for(int S=1;S<=U;S++) for(int i=0;i<n;i++){
22             if(dp[S][i]==-1)continue;
23             for(int j=0;j<n;j++) if(!(S>>j&1)&&g[i][j]) dp[S|(1<<j)][j]=max(dp[S][i]+g[i][j],dp[S|(1<<j)][j]);
24             int CS=U^S;
25             for(int j=CS;j;j=(j-1)&CS) dp[S|j][i]=max(dp[S|j][i],dp[S][i]+to[j][i]+sum[j]);
26         }printf("%lld\n",sum[U]-dp[U][n-1]);
27         return 0;
28     }
29 }
30 signed main(){return WSN::main();}

---

连续两次了，这次比上一次考得还糟糕，上次明显是T1比较傻，没想到用优先队列优化，这次更恶心

直接挂分挂到垫底要知道离真正的考试越来越近了，要是现在模拟的时候再不认真，最后你一定会后悔现在你的所做所为，

就像你今天改T2时候疯狂不知道如何打出动态开点一样傻    ，反正机会越来越少，怎么也没办法逃脱进B的事实，

原来不管是真的没有思路也好，一场因为没有关freopen也好，还是因为马虎错误挂分也好，都已经为分层的失败作出了大贡献，

而且还是不能改变的贡献。消除这些负贡献的最好方法不是考完试之后找回很快把题改完，这顶多表示你对这些题都有一定的思路，其他还有什么呢

你有思路为什么不能考场上A掉呢？为什么不能用代码实现思路呢？还是之前语言学习时候的不走心，或是当时对OI的偏见。

不过，你现在的成绩就是不理想，反映出来的就是你实力不行，就是你还无法达到标准。再怎么解释也没用，

从小就比较反感那些考完试拍大腿的人，结果也快活成那样了，要改变呀～～～。

---