[题解]Mail.Ru Cup 2018 Round 1 - D. Changing Array

【题目】

D. Changing Array

【描述】

给n个整数a[1],...,a[n]，满足0<=a[i]<=2^k-1。Vanya可以对这n个数中任一多个数进行操作，即将x变为x'，其中x'指x限制在k位内二进制取反。问a[1],...,a[n]中最多有多少个连续子段的异或和不为0。

数据范围：1<=n<=200000，1<=k<=30

【思路】

为了叙述方便，记MAX=(1<<k)-1，即二进制下k位全是1的数。

为了符号表示不产生歧义，以下使用^表示异或（上面的题目描述中指的是次方）。

这里要用到异或运算的一个很重要的性质，即x^x=0。

根据定义，x^x'=MAX，从而x'=x^x^x'=x^MAX。

先不考虑a[1],...,a[n]的变化。维护前缀异或和s[i]，于是a[i]^...^a[j]=s[j]^s[i-1]。那么，a[i]^...^a[j]==0当且仅当s[j]==s[i-1]。为了让连续子段异或和为0尽量少，就是要让s[i]尽量不同。

再看改变某个a[i]会带来的影响。将某个a[i]变为a[i]^MAX，那么包含a[i]的前缀异或和s[j]都要变为s[j]^MAX，即s[j]变为s[j]^MAX对所有j>=i。这个时候发现，如果再改变a[i+1]，则s[k]又都变回去了对所有k>=i+1。这说明可以通过改变某些a[i]实现将某一个s[j]变为s[j]^MAX。

这个时候有个很自然的想法就是，值为x和x^MAX的那些s[i]应该放在一类中考虑，因为它们最多只有两个值，要想使得“在其中挑两个数，它们不相等”的概率最小，只能让取x和x^MAX的数字个数尽量平均，即相等或者相差1。

确定s[i]的取值之后（有多少个s[i]取某个值x或者x^MAX），记第k个取值的s[i]共有nk个，于是最终的答案为。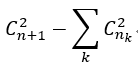

注意：要注意取值范围，要开long long！【比赛中第一次提交就因为这个问题WA了……

【我的实现】

 1 #include <iostream>
 2 #include <cstdio>
 3 #include <cstring>
 4 #include <cmath>
 5 #include <algorithm>
 6
 7 using namespace std;
 8 #define MaxN 200030
 9
10 long long s[MaxN];
11
12 int main()
13 {
14     long long n, k;
15     long long i, j;
16     long long cnt, ans, tmp;
17     long long x;
18     long long MAX;
19     //scanf("%d%d", &n, &k);
20     cin >> n >> k;
21     MAX = (1<<(long long)k)-1;
22     s[0] = 0;
23     for(i = 1; i <= n; i++)
24     {
25         cin >> x;
26         s[i] = s[i-1] ^ x;
27     }
28     for(i = 0; i <= n; i++)
29         s[i] = min(s[i], MAX^s[i]);
30     sort(s, s+n+1);
31     cnt = 0;
32     ans = (n+1) * n / 2;
33     for(i = 0; i <= n; i++)
34     {
35         if(i == 0 || s[i] == s[i-1])
36             cnt++;
37         else
38         {
39             if(cnt % 2) //奇数
40             {
41                 tmp = cnt / 2;
42                 ans -= tmp * (tmp-1) / 2;
43                 tmp = cnt / 2 + 1;
44                 ans -= tmp * (tmp-1) / 2;
45             }
46             else
47             {
48                 tmp = cnt / 2;
49                 ans -= tmp * (tmp-1);
50             }
51             cnt = 1;
52         }
53     }
54     if(cnt % 2) //奇数
55     {
56         tmp = cnt / 2;
57         ans -= tmp * (tmp-1) / 2;
58         tmp = cnt / 2 + 1;
59         ans -= tmp * (tmp-1) / 2;
60     }
61     else
62     {
63         tmp = cnt / 2;
64         ans -= tmp * (tmp-1);
65     }
66     cout<< ans;
67     return 0;
68 }

【评测结果】