BlockingQueue的基本原理

1. 前言

BlockingQueue即阻塞队列，它算是一种将ReentrantLock用得非常精彩的一种表现，依据它的基本原理，我们可以实现Web中的长连接聊天功能，当然其最常用的还是用于实现生产者与消费者模式，大致如下图所示：

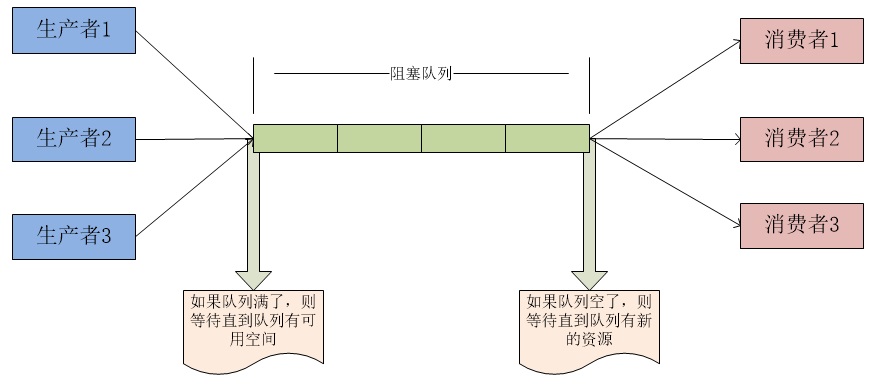
在Java中，BlockingQueue是一个接口，它的实现类有ArrayBlockingQueue、DelayQueue、 LinkedBlockingDeque、LinkedBlockingQueue、PriorityBlockingQueue、SynchronousQueue等，它们的区别主要体现在存储结构上或对元素操作上的不同，但是对于take与put操作的原理，却是类似的。下面的源码以ArrayBlockingQueue为例。

2. 分析

BlockingQueue内部有一个ReentrantLock，其生成了两个Condition，在ArrayBlockingQueue的属性声明中可以看见：

/** Main lock guarding all access */
final ReentrantLock lock;
/** Condition for waiting takes */
private final Condition notEmpty;
/** Condition for waiting puts */
private final Condition notFull;

...

public ArrayBlockingQueue(int capacity, boolean fair) {
    if (capacity <= 0)
        throw new IllegalArgumentException();
    this.items = new Object[capacity];
    lock = new ReentrantLock(fair);
    notEmpty = lock.newCondition();
    notFull =  lock.newCondition();
}

而如果能把notEmpty、notFull、put线程、take线程拟人的话，那么我想put与take操作可能会是下面这种流程：

put(e)

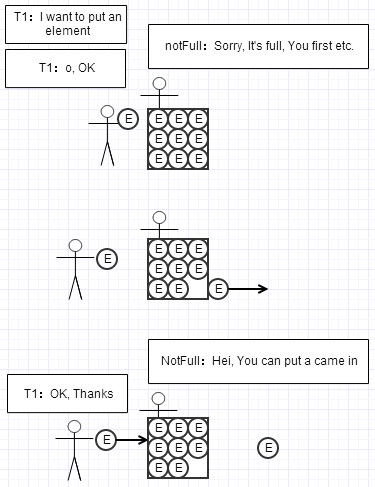
take()

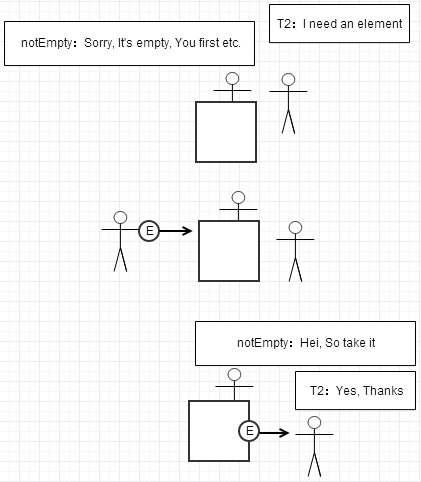
其中ArrayBlockingQueue.put(E e)源码如下（其中中文注释为自定义注释，下同）：

/**
 * Inserts the specified element at the tail of this queue, waiting
 * for space to become available if the queue is full.
 *
 * @throws InterruptedException {@inheritDoc}
 * @throws NullPointerException {@inheritDoc}
 */
public void put(E e) throws InterruptedException {
    checkNotNull(e);
    final ReentrantLock lock = this.lock;
    lock.lockInterruptibly();
    try {
        while (count == items.length)
            notFull.await(); // 如果队列已满，则等待
        insert(e);
    } finally {
        lock.unlock();
    }
}

/**
 * Inserts element at current put position, advances, and signals.
 * Call only when holding lock.
 */
private void insert(E x) {
    items[putIndex] = x;
    putIndex = inc(putIndex);
    ++count;
    notEmpty.signal(); // 有新的元素被插入，通知等待中的取走元素线程
}

ArrayBlockingQueue.take()源码如下：

public E take() throws InterruptedException {
    final ReentrantLock lock = this.lock;
    lock.lockInterruptibly();
    try {
        while (count == 0)
            notEmpty.await(); // 如果队列为空，则等待
        return extract();
    } finally {
        lock.unlock();
    }
}

/**
 * Extracts element at current take position, advances, and signals.
 * Call only when holding lock.
 */
private E extract() {
    final Object[] items = this.items;
    E x = this.<E>cast(items[takeIndex]);
    items[takeIndex] = null;
    takeIndex = inc(takeIndex);
    --count;
    notFull.signal(); // 有新的元素被取走，通知等待中的插入元素线程
    return x;
}

可以看见，put(E)与take()是同步的，在put操作中，当队列满了，会阻塞put操作，直到队列中有空闲的位置。而在take操作中，当队列为空时，会阻塞take操作，直到队列中有新的元素。

而这里使用两个Condition，则可以避免调用signal()时，会唤醒相同的put或take操作。