Codeforces Round #527 F - Tree with Maximum Cost /// 树形DP

题目大意：

给定一棵树 每个点都有点权 每条边的长度都为1

树上一点到另一点的距离为最短路经过的边的长度总和

树上一点到另一点的花费为距离乘另一点的点权

选定一点出发 使得其他点到该点的花费总和是最大的

先dfs一遍 获得 s[u] 为u点往下的点权总和（包括u点）

由其子节点v及其本身权值可得 s[u]=s[v]+w[u]

获得 dp[u] 为u点出发往下的花费总和（u点出发的花费不需要包括u点）

由其子节点v的dp[v]及s[v]可得 dp[u]=dp[v]+s[v]

再深搜一遍树形dp 获得 dp[u] 为u点出发到其他所有点的花费总和

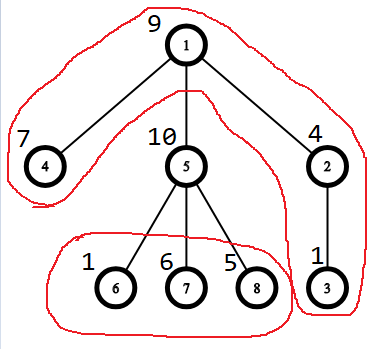
此时 fa=1 u=5

dp[fa]=dp[9]=1*(7+10+4)+2*(1+6+5+1)=(1+6+5)*2+(7+4+10)*1+1*2

dp[u]=dp[5]=1*(1+6+5+9)+2*(7+4)+3*1=(1+6+5)*1+9*1+(7+4)*2+1*3

发现由fa的结果得到u的结果需要 加上u往上的值 再减去u往下(包括u)的值

相当于 加上整棵树的值sum 再减两次u往下的值s[u] 即dp[u] = dp[fa] + sum - 2*s[u]

dp[fa]+sum-2*s[u] =(1+6+5)*2+(7+4+10)*1+1*2 + (1+6+5+7+4+10+9+1) - 2*(10+1+6+5)

　　　　　　　　=(1+6+5)*3+(7+4+10)*2+1*3+9 - 2*(10+1+6+5)

　　　　　　　　=(1+6+5)*1+(7+4)*2+1*3+9*1 = dp[u]

#include <bits/stdc++.h>
#define LL long long
#define INF 0x3f3f3f3f
using namespace std;
const int N=2e5+;
LL n, w[N];
LL ans, sum;
LL s[N], dp[N];
// s[u]为u点往下的点的权值总和
vector <int> E[N];

void dfs2(int u,int fa) {
    if(fa) dp[u]=dp[fa]+sum-*s[u];
    // 如果u存在父节点 由dp[fa]可得到dp[u]
    // 此时dp[u]为由u点出发去往其他所有点的总花费
    for(int i=;i<E[u].size();i++) {
        int v=E[u][i];
        if(v==fa) continue;
        dfs2(v,u);
    }
    ans=max(ans,dp[u]);
}
void dfs1(int u,int fa) {
    s[u]=w[u];
    for(int i=;i<E[u].size();i++) {
        int v=E[u][i];
        if(v==fa) continue;
        dfs1(v,u);
        s[u]+=s[v];
        dp[u]=dp[u]+dp[v]+s[v];
        // 此时dp[u]为由u点出发往下的总花费
    }
}

int main()
{
    while(~scanf("%I64d",&n)) {
        ans=sum=0LL;
        for(int i=;i<=n;i++) {
            scanf("%I64d",&w[i]);
            sum+=w[i]; E[i].clear();
        }
        for(int i=;i<n;i++) {
            int u,v; scanf("%d%d",&u,&v);
            E[u].push_back(v);
            E[v].push_back(u);
        }
        memset(s,,sizeof(s));
        memset(dp,,sizeof(dp));
        dfs1(,); dfs2(,);
        printf("%I64d\n",ans);
    }

    return ;
}