ACM的探索之Everything is Generated In Equal Probability! 后序补充丫!
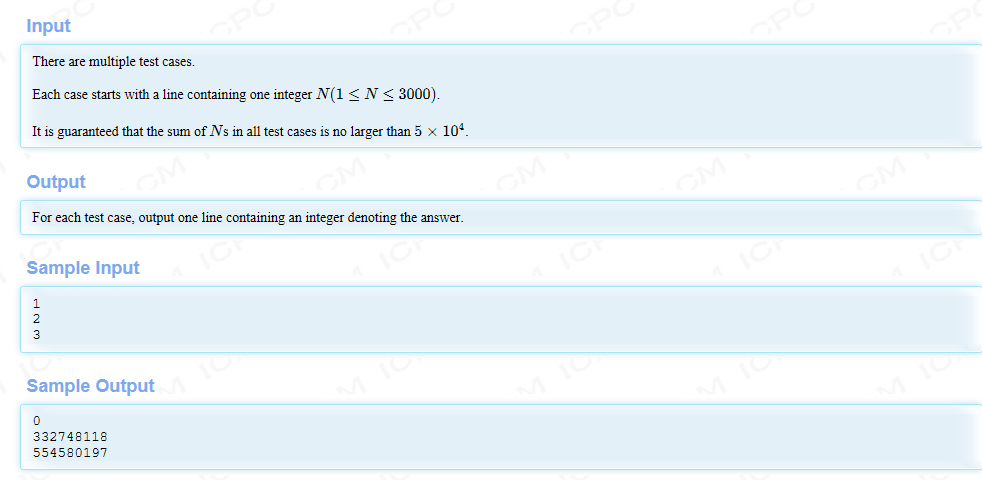
Problem Desciption:

百度翻译后的汉化:

参见博客:https://www.cnblogs.com/zxcoder/p/11253099.html
https://blog.csdn.net/Cassie_zkq/article/details/97255683https://blog.csdn.net/Cassie_zkq/article/details/97255683
ACM的探索之Everything is Generated In Equal Probability! 后序补充丫!的更多相关文章
- ACM的探索之Everything Is Generated In Equal Probability(这真的是很有趣的话语丫!)
---------------------------------------步履不停,奋勇前进! ------------------------难度真的是蛮大丫!后序补充!
- HDU 6595 Everything Is Generated In Equal Probability (期望dp,线性推导)
Everything Is Generated In Equal Probability \[ Time Limit: 1000 ms\quad Memory Limit: 131072 kB \] ...
- 【HDOJ6595】Everything Is Generated In Equal Probability(期望DP)
题意:给定一个N,随机从[1,N]里产生一个n, 然后随机产生一个n个数的全排列,求出n的逆序数对的数量并累加ans, 然后随机地取出这个全排列中的一个子序列,重复这个过程,直到为空,求ans在模99 ...
- hdu多校第二场 1005 (hdu6595) Everything Is Generated In Equal Probability
题意: 给定一个N,随机从[1,N]里产生一个n,然后随机产生一个n个数的全排列,求出n的逆序数对的数量,加到cnt里,然后随机地取出这个全排列中的一个非连续子序列(注意这个子序列可以是原序列),再求 ...
- HDU-多校2-Everything Is Generated In Equal Probability(公式+逆元)
Problem Description One day, Y_UME got an integer N and an interesting program which is shown below: ...
- [hdu6595]Everything Is Generated In Equal Probability
计算一对逆序对的贡献,即在n个数期望要删多少步才能删掉其中的两个数,设f(n)表示此时的期望,则有方程$f[n]=3/4+(\sum_{i=2}^{n}f[i]\cdot c(n-2,i-2))/2^ ...
- ACM学习历程——UVA11234 Expressions(栈,队列,树的遍历,后序遍历,bfs)
Description Problem E: Expressions2007/2008 ACM International Collegiate Programming Contest Unive ...
- ACM的探索之Keen On Evrything But Triangle(我觉得可以很接近啦!!)
#include<bits/stdc++.h> using namespace std; int main() { int n,q,l,r; while(cin>>n>& ...
- ACM的探索之Just Skip The Problem
-----------------心怀虔诚,奋勇前进,fighting!!!!!! Problem Description: inclusively: 包括一切地;包含地 simul ...
随机推荐
- 无法解析的外部符号 _snprintf
VS2010下: 在使用第三方静态库 遇到无法解析的外部符号 _snprintf . 编译第三方库的时候 看到有 warning C4013: 'snprintf' undefined; assumi ...
- 1级搭建类103-Oracle 12c 单实例 FS(12.2.0.1+RHEL 7)公开
项目文档引子系列是根据项目原型,制作的测试实验文档,目的是为了提升项目过程中的实际动手能力,打造精品文档AskScuti. 项目文档引子系列目前不对外发布,仅作为博客记录.如学员在实际工作过程中需提前 ...
- 洛谷P1551 亲戚 (并查集模板题)
链接 https://www.luogu.org/problemnew/show/P1551 代码 #include<bits/stdc++.h> using namespace std; ...
- Flask知识总结
1.-----------------路由设置的2种方式----------------- 查看源码,route方法里,本质是执行app.add_url_rule() 因此可以这么写(主流方式): @ ...
- MyEclipse-2017破解过程
下载 myeclipse2017百度云下载路径: 链接:https://pan.baidu.com/s/1wQYwO2zrUvbbUcjCB5B8IQ 密码:6igu myeclipse2017破解文 ...
- PHP返回json数据为null
文件编码非utf-8,导致json_encode()返回false:最后前台ajax接收不到数据
- 关于 RMAN 控制文件自动备份路径中指定的 %F 说明
默认情况下,RMAN备份的属性配置一共 14 行( show all; )来自博客园AskScuti CONFIGURE CONTROLFILE AUTOBACKUP FORMAT FOR DEVIC ...
- Mac使用pip命令安装selenium包报错解决方法
1.使用命令: pip install selenium 2.换成命令: python -m pip install selenium 即可成功安装
- 虚拟机中CentOS 6.5 添加扩展分区
此扩展方法要求支持LVM 1.更改虚拟机配置 虚拟机->设置->硬盘->扩展磁盘容量 fdisk -l 查看,发现硬盘空间变大了 [root@thj Desktop]# fdisk ...
- 记录 shell学习过程(3) if 的格式
] #-e 为检测目录或文件是否存在 !为取反 then mkdir -v /tmp/ echo 'ok' fi if else if [ $USER == 'root' ] then echo 'h ...
