Leetcode Week4 Find Minimum in Rotated Sorted Array II

Question

Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand.

(i.e.,  [0,1,2,4,5,6,7] might become  [4,5,6,7,0,1,2]).

Find the minimum element.

Answer

借用以下网上的翻译：

　　把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。 输入一个非减排序的数组的一个旋转，输出旋转数组的最小元素。 例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转，该数组的最小值为1。 NOTE：给出的所有元素都大于0，若数组大小为0，请返回0。

　　下面我们来解题：

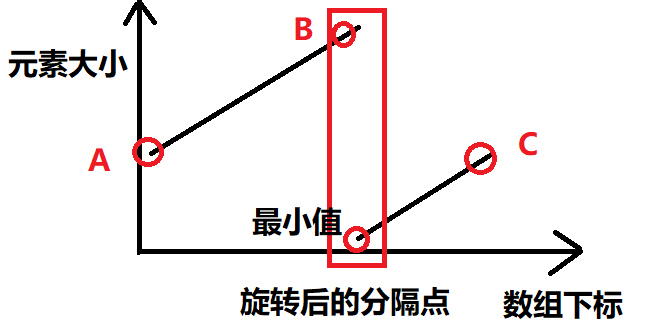
　　最初可以通过画图理解，我想或许我们可以画着以下的图（为了方便，离散点画成连续的）：

　　当然这个草图也真是草图，很粗糙，哈哈，而且不能解释所有情况，它只能解决严格递增。不过，这应该能解决大部分情况，至于其它小部分的情况我们等下再考虑。

主要思路

　　我们头脑第一个蹦出来的想法或许就是遍历一次取最小值就好，这很简单，也很容易实现，但这显然不是我们想要的，时间复杂度为O（n)。

　　我们想另外一种方法。非减？有序？有没有觉得有点像二分查找，只不过它被分成两截了，不过这并不能难倒我们，我们不妨试着用这思路解决。

　　相对于二分查找，我们没有所要查找的目标，数组也不是完全有序。不过，我们想想如何模仿这种过程，二分查找是取中间值来跟目标值比较进而缩小范围的，而我们这题如何缩小范围呢，取什么比较呢，如果取中间值，又和谁比较呢。靠直觉，我们取最初点（设为A）、最后一个点（设为C），与中间点（设为B）比较，因为这三个点最具代表性，对于A与C来说，很显然A>=C，我们再分析B，B可能在左半边直线上，也有可能在右半边直线；如果在左半边直线，这时候B>=A>=C，这时候可以断定最小值在B-C之间，因为B-C不是连续递增的；如果在右半边直线，这时候A>=C>=B，可以断定最小值在A-B之间，因为A-B之间不是连续递增的，肯定在某个地方有个“坑”。总结一下，如果B>C，就继续在B-C查找，如果A>B，则在A-C查找。

　　我们还需要个终止条件，就是让这个查找终止下来。我们通过上面的算法不断缩小搜索范围，最终肯定缩小到两个元素，因为如果存在三个元素以上，中间值是取除边界两个点（A，C)外的其中一个点，这样下次搜索范围能继续缩小，直到两个点。最后我们需要得到最小值，而两个元素必然存在着最小值，但哪个是最小值呢，为了避免麻烦，我们可以比较一次得出最小值。

　（括号可以不看，单纯说下我最初考虑两个值种取最小值的过程，A与C之间的范围逐渐缩小，逐渐逼近最小值，最后剩下的两个点的分布有两种可能，一种是分别在一条直线上，另一种可能是都在右半条直线上，然后，我们细想这个逼近的过程是可以排除第二种可能的，因为点A是不会随着搜索范围的减少而到达下面那条直线的。因此，只会分别在一条直线上，从图上来看两个点恰好是一上一下，这样我们取下面那点，就是那个数组下标偏大的那个点即可，不过这会在我们没有讨论过的一些特例里失效，比如旋转数组为[1,2]，因为这不符合我们上面讨论的模型，因为[1,2]全部旋转了，回到最初的位置，元素位置并没有变化，因此我们采用比较两个元素的方法得到最小值比较好）

　　所以我们能像二分查找那样写出大致以下的代码：

    int findMinVal(int min, int max, const vector<int> &rotateArray) {
        // 取三个点的值
        int minVal = rotateArray[min];             //最左边的点的值
        int maxVal = rotateArray[max];             //最右边的点的值
        int midVal = rotateArray[(min + max) / ]; //中间的点的值

        // 终止条件
　　　　　　if ((max - min) <= )
　　　　　　　　return minVal > maxVal ? maxVal : minVal;

        // 根据三个点的值缩小搜索范围
        if (midVal > maxVal)
            return findMinVal((min + max) / , max, rotateArray);
        else if (minVal > midVal)
            return findMinVal(min, (min + max) / , rotateArray);

        // 先无视这个return先，等等再讨论
        return minVal;
    }

考虑特殊情况

　　如果我们放上Leetcode提交，这肯定是过不了的。如果你是个谨慎的人，一定会想到有各种特殊情况，特别是三个点的值之间存在相等关系的时候。我们下面就来考虑这些情况。

　　首先是如果midVal > maxVal或者minVal > midVal，那么在所有情况下都是能正确的缩小搜索范围的，这就不讨论了。
　　所以我们剩下要讨论的情况是midVal <= maxVal 且 minVal <= midVal，组合起来就是minVal <= midVal <= maxVal。我们分四种情况考虑 。

　　①minVal < midVal < maxVal，这种情况存在于像[1,2,3]完全旋转后和最初数组一样的数组。这种很明显取minVal即可。

②minVal < midVal = maxVal，这种和①一样，例如数组为[1,2,2]，取minVal即可。

③minVal = midVal < maxVal,  同①，例如[1,1,2]，取minVal即可。

④minVal = midVal = maxVal,  这种情况有些特殊，不能缩小一半的范围，也不能得出最小值，例如[1,1,0,1]或[1,1,0,1,1,1,1]，所以只能一步一步缩小，即将索引min+1,max-1。

　　①-③可以合并。最终代码如下：

　　

    int findMin(vector<int>& nums) {
         if (nums.empty())
            return ;
        return findMinVal(, nums.size() - , nums);
    }

    int findMinVal(int min, int max, const vector<int> &rotateArray) {

        int minVal = rotateArray[min];
        int maxVal = rotateArray[max];
        int midVal = rotateArray[(min + max) / ];
        if ((max - min) <= )
            return minVal > maxVal ? maxVal : minVal;
        if (midVal > maxVal)
            return findMinVal((min + max) / , max, rotateArray);
        else if (minVal > midVal)
            return findMinVal(min, (min + max) / , rotateArray);
        else if (minVal == midVal && midVal == maxVal)
            return findMinVal(min+1, max-1, rotateArray);
        return minVal;
    }

　　由于上面的讨论缺乏严格完整的数学证明过程，我不敢保证能考虑到所有情况，如果有漏了某些情况，请告诉我= =，哈哈。不过是能通过leetcode和牛客网的检测的。