洛谷P1140 相似基因 (DP)

洛谷P1140 相似基因

题目背景

大家都知道，基因可以看作一个碱基对序列。它包含了44种核苷酸，简记作A,C,G,TA,C,G,T。生物学家正致力于寻找人类基因的功能，以利用于诊断疾病和发明药物。

在一个人类基因工作组的任务中，生物学家研究的是：两个基因的相似程度。因为这个研究对疾病的治疗有着非同寻常的作用。

题目描述

两个基因的相似度的计算方法如下：

对于两个已知基因，例如AGTGATGAGTGATG和GTTAGGTTAG，将它们的碱基互相对应。当然，中间可以加入一些空碱基-，例如：

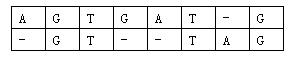
这样,两个基因之间的相似度就可以用碱基之间相似度的总和来描述，碱基之间的相似度如下表所示：

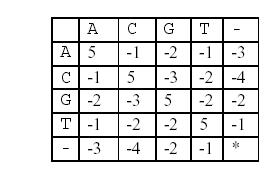
那么相似度就是：(-3)+5+5+(-2)+(-3)+5+(-3)+5=9(−3)+5+5+(−2)+(−3)+5+(−3)+5=9。因为两个基因的对应方法不唯一，例如又有：

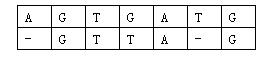
相似度为：(-3)+5+5+(-2)+5+(-1)+5=14(−3)+5+5+(−2)+5+(−1)+5=14。规定两个基因的相似度为所有对应方法中，相似度最大的那个。

输入输出格式

输入格式：

共两行。每行首先是一个整数，表示基因的长度；隔一个空格后是一个基因序列，序列中只含A,C,G,TA,C,G,T四个字母。1 \le1≤序列的长度\le 100≤100。

输出格式：

仅一行，即输入基因的相似度。

输入输出样例

输入样例#1：

7 AGTGATG

5 GTTAG

输出样例#1：

14

Solution

显然二维dp?

设\(dp[i][j]\)表示字符串1匹配到i字符串2匹配到j(不包含'-')的最高得分

那么对于每个状态,就有三种情况,我们把这三种情况列出来,状态转移方程也就差不多了

1. 当前i不动,由j去匹配'-'
2. 当前j不动,有i去匹配'-'
3. 当前i匹配当前j

为了方便转移,我们把每个配对的得分列成表

int cost[6][6]={
    {0},
    {0,5,-1,-2,-1,-3},
    {0,-1,5,-3,-2,-4},
    {0,-2,-3,5,-2,-2},
    {0,-1,-2,-2,5,-1},
    {0,-3,-4,-2,-1,-inf},
};

那么其实状态转移方程也就出来了

\[dp[i][j]=max(dp[i][j],dp[i][j-1]+cost[b[j]][5])
\]

\[dp[i][j]=max(dp[i][j],dp[i-1][j])+cost[a[i]][5]
\]

\[dp[i][j]=max(dp[i][j],dp[i-1][j-1]+cost[a[i]][b[j]])
\]

初始化

    for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)dp[i][j]=-inf;
    for(int i=1;i<=n;i++) dp[i][0]=dp[i-1][0]+cost[a[i]][5];//i不匹配
    for(int i=1;i<=m;i++) dp[0][i]=dp[0][i-1]+cost[b[i]][5];//j不匹配

Code

#include<bits/stdc++.h>
using namespace std;
const int inf=2e9;
int n,m,dp[110][110],a[110],b[110];
string s1,s2;
int cost[6][6]={
    {0},
    {0,5,-1,-2,-1,-3},
    {0,-1,5,-3,-2,-4},
    {0,-2,-3,5,-2,-2},
    {0,-1,-2,-2,5,-1},
    {0,-3,-4,-2,-1,-inf},
};
int main()
{
    ios::sync_with_stdio(0);
    cin>>n>>s1>>m>>s2;
    for(int i=1;i<=n;i++)
        switch(s1[i-1]) {
        case 'A':a[i]=1;break;
        case 'C':a[i]=2;break;
        case 'G':a[i]=3;break;
        case 'T':a[i]=4;break;
        }
    for(int i=1;i<=m;i++)
        switch(s2[i-1]) {
        case 'A':b[i]=1;break;
        case 'C':b[i]=2;break;
        case 'G':b[i]=3;break;
        case 'T':b[i]=4;break;
        }
    for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)dp[i][j]=-inf;
    for(int i=1;i<=n;i++) dp[i][0]=dp[i-1][0]+cost[a[i]][5];
    for(int i=1;i<=m;i++) dp[0][i]=dp[0][i-1]+cost[b[i]][5];
    for(int i=1;i<=n;i++) {
        for(int j=1;j<=m;j++) {
            dp[i][j]=max(dp[i][j],dp[i][j-1]+cost[b[j]][5]);
            dp[i][j]=max(dp[i][j],dp[i-1][j]+cost[a[i]][5]);
            dp[i][j]=max(dp[i][j],dp[i-1][j-1]+cost[a[i]][b[j]]);
        }
    }
    cout<<dp[n][m]<<endl;//目标状态
}

博主蒟蒻,随意转载.但必须附上原文链接

http://www.cnblogs.com/real-l/