[CSP-S模拟测试]:sum（数学+莫队）

题目传送门（内部题63）

---

输入格式

第一行有一个整数$id$，表示测试点编号。
第一行有一个整数$q$，表示询问组数。
然后有$q$行，每行有两个整数$n_i,m_i$。

---

输出格式

一共有$q$行，每行一个整数表示每组询问的答案$S_{n_i,m_i}$对$10^9+7$取模的结果。

---

样例

样例输入：

1
5
1 1
2 1
3 2
4 3
5 5

样例输出：

2
3
7
15
32

---

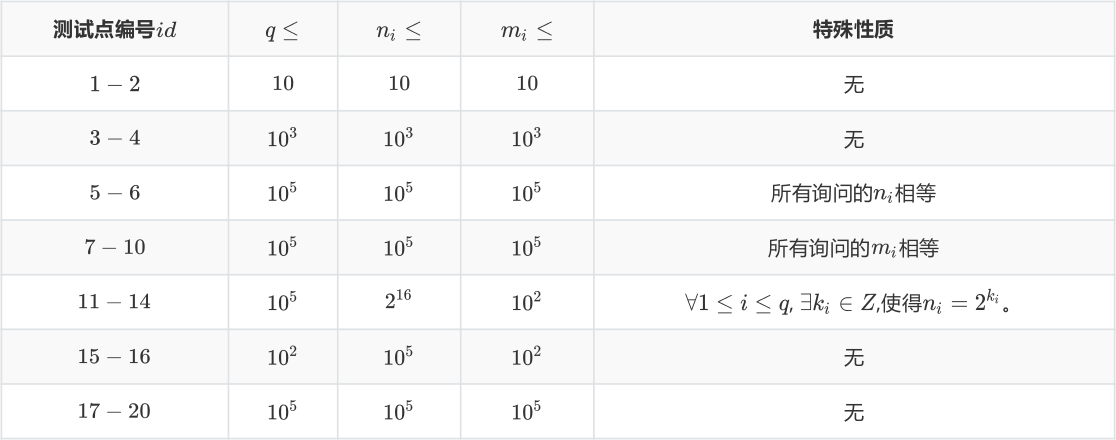
数据范围与提示

对于所有数据，$1\leqslant q,n_i,m_i\leqslant 10^5$。

---

题解

考场上把$80$分部分分都水全了，愣是没想到莫队……

先来考虑所有询问的$n_i$相等应该怎么办，预处理即可，考虑$S_{n,m-1}$如何转移到$S_{n,m}$，无非就是加上$C_n^m$即可，不再赘述。

现在考虑所有询问的$m_i$相等应该怎么办，显然预处理没有那么简单，考虑$S_{n-1,m}$如何转移到$S_{n,m}$，既然组合数可以用杨辉三角推得，不妨画个杨辉三角。

为方便，我现在只画出杨辉三角中的其中两行为例

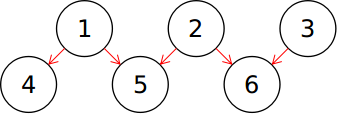
设$1$号点为$n-1$行的行首，$4$号点为$n$行的行首，利用杨辉三角的性质，编号为$4$的点等于编号为$1$的点，编号为$5$的点等于编号为$1$的点和编号为$2$的点的加和，编号为$6$的点等于编号为$2$的点和编号为$3$的点的加和。

还可以发现，在从$n-1$行向$n$行转移的时候除了$3$号点以外其它点都被加了$2$次，只有$3$号点只加了$1$次，那么我们可以得出$S_{n,m}=S_{n-1,m}*2-C_{n-1}^m$，同理$S_{n-1,m}=\frac{S_{n,m}+C_{n-1}^m}{2}$。

利用这个性质我们就可以解决这个子问题了。

得出了这些性质，我们可以考虑莫队算法，$m$相当于$l$，$n$相当于$r$，这道题就解决了。

时间复杂度：$\Theta(n\sqrt{n})$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
struct rec{int n,m,id,pos;}e[100001];
const int mod=1000000007;
const int inx=500000004;
int q;
long long ans[100001];
long long jc[100001],inv[100001];
long long qpow(long long x,long long y)
{
	long long res=1;
	while(y)
	{
		if(y%2)res=res*x%mod;
		y>>=1;
		x=x*x%mod;
	}
	return res;
}
void pre_work()
{
	jc[0]=1;
	for(long long i=1;i<=100000;i++)
		jc[i]=jc[i-1]*i%mod;
	inv[100000]=qpow(jc[100000],mod-2);
	for(int i=100000;i;i--)
		inv[i-1]=inv[i]*i%mod;
}
long long get_C(long long x,long long y){return jc[x]*inv[y]%mod*inv[x-y]%mod;}
long long lucas(long long x,long long y)
{
	if(!y)return 1;
	return get_C(x%mod,y%mod)*lucas(x/mod,y/mod)%mod;
}
bool cmp(rec a,rec b){return (a.pos)^(b.pos)?a.m<b.m:(((a.pos)&1)?a.n<b.n:a.n>b.n);}
int main()
{
	pre_work();int mxn=0;
	scanf("%d%d",&q,&q);
	for(int i=1;i<=q;i++)
	{
		scanf("%d%d",&e[i].n,&e[i].m);
		mxn=max(mxn,e[i].n);e[i].id=i;
	}
	int t=sqrt(mxn);
	for(int i=1;i<=q;i++)e[i].pos=(e[i].m-1)/t+1;
	sort(e+1,e+q+1,cmp);
	int m=0,n=0;
	long long now=1;
	for(int i=1;i<=q;i++)
	{
		while(n<e[i].n)now=(now*2%mod-lucas(n++,m)+mod)%mod;
		while(m<e[i].m)now=(now+lucas(n,++m))%mod;
		while(m>e[i].m)now=(now-lucas(n,m--)+mod)%mod;
		while(n>e[i].n)now=(now+lucas(--n,m))*inx%mod;
		ans[e[i].id]=now;
	}
	for(int i=1;i<=q;i++)printf("%lld\n",ans[i]);
	return 0;
}

---

rp++