【CF1243C】 Tile Painting【思维】

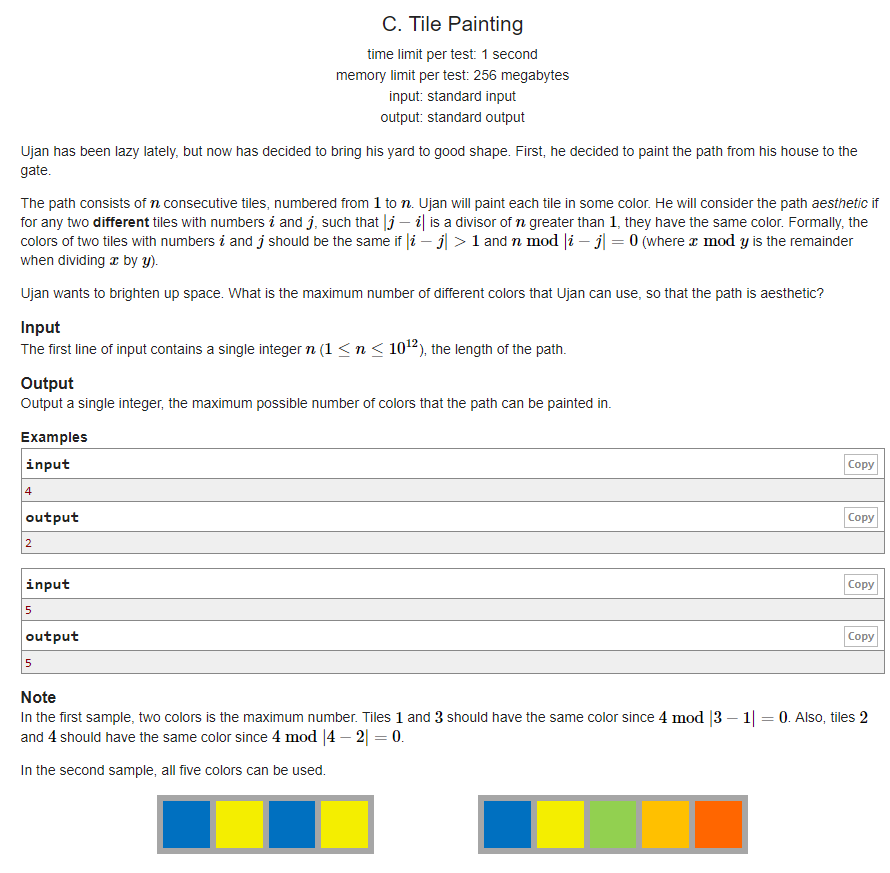
题意：给定长度为n的方块，要求染色，需要满足：当|j-i|>1且n%|j-i|==0时，两格颜色相同，求做多可以染多少种颜色

题解：求出n的所有质因子

1、若只有一种质因子，则答案为该质因子

2、若有两种以上的质因子，则答案为1

只有一种质因子时，相当于每隔若干个放同种颜色，则可以放p种颜色

有两种以上的质因子时，选取最小的两个质因子，那么只需要长度lcm(p1,p2)的格子，就可以让所有位置变成相同的颜色，且p1,p2是n的质因子，故lcm(p1,p2)≤n

#include<iostream>
#include<cstdio>
#include<cstdlib>
#define ll long long
using namespace std;
ll n;
int pn;
ll p[];
int main()
{
    scanf("%I64d",&n);ll t=n;
    for(ll i=;i<=;i++)
    {
      if(n%i==)
      {
        p[++pn]=i;
        while(n%i==)n/=i;
      }
      if(n<i)break;
    }
    if(n>)p[++pn]=n;
    if(pn==)return !printf("%I64d\n",p[]);
    return !printf("1\n");
}