EM算法（4）：EM算法证明

目录

EM算法（1）：K-means 算法

EM算法（2）：GMM训练算法

EM算法（3）：EM算法运用

EM算法（4）：EM算法证明

　　　　　　　　

　　　　　　　　　　　　　　　　　　EM算法（4）：EM算法证明

1. 概述

　　上一篇博客我们已经讲过了EM算法，EM算法由于其普适性收到广泛关注，高频率地被运用在各种优化问题中。但是EM算法为什么用简单两步就能保证使得问题最优化呢？下面我们就给出证明。

2. 证明

　　现在我们已经对EM算法有所了解，知道其以两步（E-step和M-step）为周期，迭代进行，直到收敛为止。那问题就是，在一个周期内，目标函数的值是否增加了？如果能保证其每个周期都在增加的话，那么其必然收敛到一个局部最大值处。这就是我们EM算法所需要证明的，即：

　　　　　　　　　　　　$p(\mathbf{X};\theta^{(i+1)}) \geqslant p(\mathbf{X};\theta^{(i)})$

　　首先假设Y的分布为$q(\mathbf{Y})$，则有$\sum_Yq(\mathbf{Y}) = 1$，则：

　　　　　　

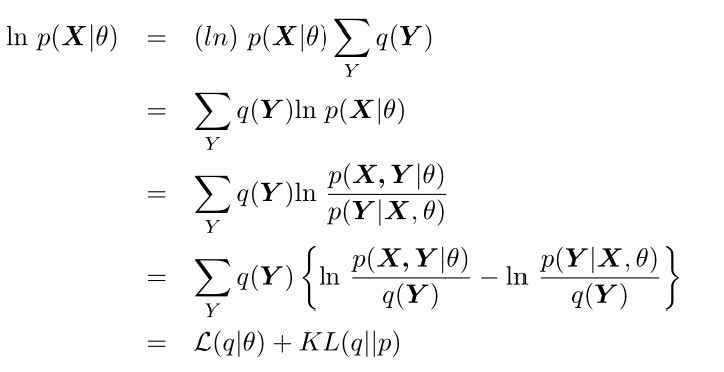
　　现在假设在EM算法第i个周期结束，因为KL(q||p)不小于零，那么其最小时就为0，即$q(\mathbf{Y})=p(\mathbf{Y}|\mathbf{X},\theta^{(i)})$时。

　　在E-step时，我们计算$Q(\theta^{(i+1)}|\theta^{(i)})$，我们发现：

　　　　　　　　

　　在M-step时，我们找到一个$\theta^{(i+1)}$，使得$Q(\theta|\theta^{(i)})$最大，即也是使得$\mathcal{L}(q|\theta)$最大。同时，因为此时$p(\mathbf{X,Y}|\theta^{(i+1)}) \neq p(\mathbf{X,Y}|\theta^{(i)}) = q(\mathbf{Y})$，那么KL(q||p)也会大于零。那么相对于第i个EM周期结束时的目标函数的值，现在其两个和项的值都是非减的，那么很容易得到：

　　　　　　　　　　　　$p(\mathbf(X)|\theta^{(i+1)}) \geqslant p(\mathbf{X}|\theta^{(i)})$