ML之监督学习算法之分类算法一 ——

一、概述

　　决策树（decision tree）的一个重要任务是为了数据中所蕴含的知识信息，因此决策树可以使用不熟悉的数据集合，并从中提取出一系列规则，在这些机器根据数据创建规则时，就是机器学习的过程。

二、决策树的构造

　　决策树：

　　　　优点：计算复杂度不高，输出结果易于理解，对中间值的缺失不敏感，可以处理不相关特征数据。

　　　　缺点：可能会产生过度匹配问题。

　　适用数据类型：数值型和标称型

　　在构造决策树时，我们需要解决的第一个问题就是，当前数据集上哪个特征在划分数据分类时起决定性作用。为了找到决定性的特征，划分出最好的结果，我们必须评估每个特征。完成测试之后，原始数据集就被划分为几个数据子集。这些数据子集会分布在第一个决策点的所有分支上；

　　决策树的一般流程
　　　　1. 收集数据：可以使用任何方法。
　　　　2. 准备数据：树构造算法只适用于标称型数据，因此数值型数据必须离散化。
　　　　3. 分析数据：可以使用任何方法，构造树完成之后，我们应该检查图形是否符合预期。
　　　　4. 训练算法：构造树的数据结构。
　　　　5. 测试算法：使用经验树计算错误率。
　　　　6. 使用算法：此步骤可以适用于任何监督学习算法，而使用决策树可以更好地理解数据的内在含义。

　　涉及的算法：

　　　　二分法：一些决策树算法采用二分法划分数据，

　　　　ID3：而我们将适用ID3算法划分数据集，ID3算法更多信息了解

　　　　C4.5： ID3的一个改进，比ID3准确率高且快，可以处理连续值和有缺失值的feature

　　　　CRAT：使用基尼指数的划分准则，通过在每个步骤最大限度降低不纯洁度， CART能够处理孤立点以及对空缺值的处理；

　信息增益：

　　划分数据集的大原则是：将无序的数据变得更加有序。我们可以使用多种方法划分数据集，但是每种方法都有各自的优缺点。组织杂乱无章数据的一种方法就是使用信息论度量信息，信息论是量化处理信息的分支科学。我们可以在划分数据前后使用信息论量化度量信息的内容。
　　在划分数据集之前之后信息发生的变化称为信息增益，知道如何计算信息增益，我们就可以计算每个特征值划分数据集获得的信息增益，获得信息增益最高的特征就是最好的选择。
　熵：
　　为了计算熵（entropy），我们需要计算所有类别所有可能值包含的信息期望值，通过下面的公式得到：

　　

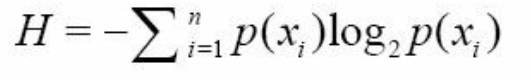
　　符号xi 的信息定义为：

　　其中p(xi)是选择该分类的概率

　　熵的单位是bit，用来衡量信息的多少；从计算熵的公式来看：

　　　　变量的不确定性越大，熵就越大；

　　计算完信息熵后，我们便可以得到数据集的无序程度。我们将对每个特征划分数据集的结果计算一次信息熵，然后判断哪个特征划分数据集是最好的划分方式（根据信息熵判断，信息熵越小，说明划分效果越好）

三、ID3算法

　　选择属性判断节点；

　　信息获取量（Information Gain）： Gain（A）= Info（D） - Infor_A(D) , 通过A来作为节点分类获取了多少信息；　　