POJ 2785 4 Values whose Sum is 0（折半枚举+二分）

4 Values whose Sum is 0

Time Limit: 15000MS		Memory Limit: 228000K
Total Submissions: 25675		Accepted: 7722
Case Time Limit: 5000MS

Description

The SUM problem can be formulated as follows: given four lists A, B, C, D of integer values, compute how many quadruplet (a, b, c, d ) ∈ A x B x C x D are such that a + b + c + d = 0 . In the following, we assume that all lists have the same size n .

Input

The first line of the input file contains the size of the lists n (this value can be as large as 4000). We then have n lines containing four integer values (with absolute value as large as 2²⁸ ) that belong respectively to A, B, C and D .

Output

For each input file, your program has to write the number quadruplets whose sum is zero.

Sample Input

6
-45 22 42 -16
-41 -27 56 30
-36 53 -37 77
-36 30 -75 -46
26 -38 -10 62
-32 -54 -6 45

Sample Output

5

Hint

Sample Explanation: Indeed, the sum of the five following quadruplets is zero: (-45, -27, 42, 30), (26, 30, -10, -46), (-32, 22, 56, -46),(-32, 30, -75, 77), (-32, -54, 56, 30).

Source

Southwestern Europe 2005

 

　　ForwardIter lower_bound(ForwardIter first, ForwardIter last,const _Tp& val)算法返回一个非递减序列[first, last)中的第一个大于等于值val的位置。

     ForwardIter upper_bound(ForwardIter first, ForwardIter last, const _Tp& val)算法返回一个非递减序列[first, last)中第一个大于val的位置。

     lower_bound和upper_bound如下图所示：

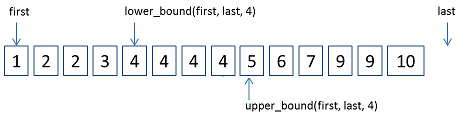
题意：

给定各有n个整数的四个数列A、B、C、D。要从每个数列中各取出1个数，使四个数的和为0。求出这样的组合的个数。当一个数列中有多个相同的数字时，把它们作为不同的数字看待。

分析：

所有全都判断一遍不可行。不过将它们对半分成AB和CD再考虑，就可以快速解决了。从2个数列中选择的话只有n2种组合，所以可以进行枚举。先从A、B中取出a、b后，为了使总和为0则需要从C、D中取出c + d = a - b。因此先将从C、D中取数字的n2种方法全部枚举出来，将这些和排好序，这样就可以运用二分搜索了。

 #include <cstdio>
 #include <algorithm>
 using namespace std;
 typedef long long ll;
 const int maxn =  + ;

 int n;
 ll a[maxn], b[maxn], c[maxn], d[maxn];
 ll cd[maxn * maxn];    //C和D中数字的组合方法  

 void solve()
 {
     //枚举从C和D中取出数字的所有方法
     for (int i = ; i < n; i++)
     {
         for (int j = ; j < n; j++)
         {
             cd[i * n + j] = c[i] + d[j];
         }
     }
     sort(cd, cd + n * n);

     ll res = ;
     for (int i = ; i < n; i++)
     {
         for (int j = ; j < n; j++)
         {
             int CD = -(a[i] + b[j]);
             //取出C和D中和为CD的部分
             //二分搜索
             res += upper_bound(cd, cd + n * n, CD) - lower_bound(cd, cd + n * n, CD);//    可能有多个答案
             //lower_bound(first, last, const _Tp& val)算法返回一个非递减序列[first, last)中的第一个大于等于值val的位置。
             //upper_bound(first, last, const _Tp& val)算法返回一个非递减序列[first, last)中第一个大于val的位置。
         }
     }
     printf("%lld\n", res);
 }

 int main()
 {
     scanf("%d", &n);
     for (int i = ; i < n; i++)
     {
         scanf("%lld%lld%lld%lld", &a[i], &b[i], &c[i], &d[i]);
     }
     solve();
     return ;
 }