【POJ】1523 SPF（割点）

http://poj.org/problem?id=1523

太弱。。。

too weak。。

割点我都还要看书和看题解来写。。果然是写不出么。。

割点就那样求，然后分量直接这个节点有多少子树就有子树个数+1个分量。还要注意root的特判。。sigh。。就是崩这里了。

#include <cstdio>
#include <cstring>
#include <cmath>
#include <string>
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
#define rep(i, n) for(int i=0; i<(n); ++i)
#define for1(i,a,n) for(int i=(a);i<=(n);++i)
#define for2(i,a,n) for(int i=(a);i<(n);++i)
#define for3(i,a,n) for(int i=(a);i>=(n);--i)
#define for4(i,a,n) for(int i=(a);i>(n);--i)
#define CC(i,a) memset(i,a,sizeof(i))
#define read(a) a=getint()
#define print(a) printf("%d", a)
#define dbg(x) cout << (#x) << " = " << (x) << endl
#define printarr2(a, b, c) for1(_, 1, b) { for1(__, 1, c) cout << a[_][__]; cout << endl; }
#define printarr1(a, b) for1(_, 1, b) cout << a[_] << '\t'; cout << endl
inline const int getint() { int r=0, k=1; char c=getchar(); for(; c<'0'||c>'9'; c=getchar()) if(c=='-') k=-1; for(; c>='0'&&c<='9'; c=getchar()) r=r*10+c-'0'; return k*r; }
inline const int max(const int &a, const int &b) { return a>b?a:b; }
inline const int min(const int &a, const int &b) { return a<b?a:b; }

const int N=2005;
int ihead[N], cnt, rt, iscut[N], FF[N], LL[N], fa[N], tot;
struct ED { int to, next; }e[N*N];
void add(int u, int v) {
	e[++cnt].next=ihead[u]; ihead[u]=cnt; e[cnt].to=v;
	e[++cnt].next=ihead[v]; ihead[v]=cnt; e[cnt].to=u;
}
void tarjan(int u, int fa) {
	FF[u]=LL[u]=++tot;
	int child=0;
	for(int i=ihead[u]; i; i=e[i].next) {
		int v=e[i].to;
		if(!FF[v]) {
			tarjan(v, u);
			++child;
			if(LL[v]>=FF[u]) ++iscut[u]; //dbg(iscut[u]); dbg(u);
			LL[u]=min(LL[v], LL[u]);
		}
		else if(FF[v]<FF[u] && fa!=v) LL[u]=min(LL[u], FF[v]);
	}
	if(child==1 && fa==-1) iscut[u]=0;
	else if(child>1 && fa==-1) iscut[u]=child-1; //特判
}

int main() {
	int u, v, cs=0;
	while(1) {
		u=getint(); if(u==0) break;
		v=getint();
		CC(ihead, 0); CC(iscut, 0); cnt=tot=0; CC(FF, 0); CC(LL, 0);
		++cs;
		add(u, v); rt=max(rt, v);
		while(1) {
			u=getint(); if(u==0) break;
			v=getint();
			add(u, v); rt=max(rt, v);
		}
		for1(i, 1, rt) if(ihead[i] && !FF[i]) tarjan(i, -1);
		// for1(i, 1, rt) if(hav[i] && iscut[i]) printf("%d\n", i);
		int flag=0;
		printf("Network #%d\n", cs);
		for1(i, 1, rt) if(iscut[i]) printf("  SPF node %d leaves %d subnets\n", i, iscut[i]+1), flag=1;
		if(!flag) puts("  No SPF nodes");
		puts("");
	}
	return 0;
}

---

Description

Consider the two networks shown below. Assuming that data moves around these networks only between directly connected nodes on a peer-to-peer basis, a failure of a single node, 3, in the network on the left would prevent some of the still available nodes from communicating with each other. Nodes 1 and 2 could still communicate with each other as could nodes 4 and 5, but communication between any other pairs of nodes would no longer be possible.

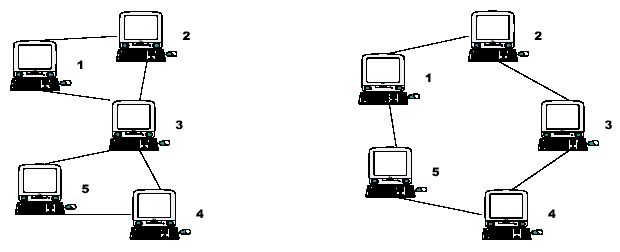
Node 3 is therefore a Single Point of Failure (SPF) for this
network. Strictly, an SPF will be defined as any node that, if
unavailable, would prevent at least one pair of available nodes from
being able to communicate on what was previously a fully connected
network. Note that the network on the right has no such node; there is
no SPF in the network. At least two machines must fail before there are
any pairs of available nodes which cannot communicate.

Input

The
input will contain the description of several networks. A network
description will consist of pairs of integers, one pair per line, that
identify connected nodes. Ordering of the pairs is irrelevant; 1 2 and 2
1 specify the same connection. All node numbers will range from 1 to
1000. A line containing a single zero ends the list of connected nodes.
An empty network description flags the end of the input. Blank lines in
the input file should be ignored.

Output

For each network in the input, you will output its number in the file, followed by a list of any SPF nodes that exist.

The first network in the file should be identified as "Network #1",
the second as "Network #2", etc. For each SPF node, output a line,
formatted as shown in the examples below, that identifies the node and
the number of fully connected subnets that remain when that node fails.
If the network has no SPF nodes, simply output the text "No SPF nodes"
instead of a list of SPF nodes.

Sample Input

1 2
5 4
3 1
3 2
3 4
3 5
0

1 2
2 3
3 4
4 5
5 1
0

1 2
2 3
3 4
4 6
6 3
2 5
5 1
0

0

Sample Output

Network #1
  SPF node 3 leaves 2 subnets

Network #2
  No SPF nodes

Network #3
  SPF node 2 leaves 2 subnets
  SPF node 3 leaves 2 subnets

Source

Greater New York 2000