[BZOJ]1019 汉诺塔(SHOI2008)

　　找规律成功次数++。

Description

　　汉诺塔由三根柱子（分别用A B C表示）和n个大小互不相同的空心盘子组成。一开始n个盘子都摞在柱子A上，大的在下面，小的在上面，形成了一个塔状的锥形体。

　　对汉诺塔的一次合法的操作是指：从一根柱子的最上层拿一个盘子放到另一根柱子的最上层，同时要保证被移动的盘子一定放在比它更大的盘子上面（如果移动到空柱子上就不需要满足这个要求）。我们可以用两个字母来描述一次操作：第一个字母代表起始柱子，第二个字母代表目标柱子。例如，AB就是把柱子A最上面的那个盘子移到柱子B。汉诺塔的游戏目标是将所有的盘子从柱子A移动到柱子B或柱子C上面。有一种非常简洁而经典的策略可以帮助我们完成这个游戏。首先，在任何操作执行之前，我们以任意的次序为六种操作（AB、AC、BA、BC、CA和CB）赋予不同的优先级，然后，我们总是选择符合以下两个条件的操作来移动盘子，直到所有的盘子都从柱子A移动到另一根柱子：（1）这种操作是所有合法操作中优先级最高的；（2）这种操作所要移动的盘子不是上一次操作所移动的那个盘子。可以证明，上述策略一定能完成汉诺塔游戏。现在你的任务就是假设给定了每种操作的优先级，计算按照上述策略操作汉诺塔移动所需要的步骤数。

Input

　　输入有两行。第一行为一个整数n，代表盘子的个数。第二行是一串大写的ABC字符，代表六种操作的优先级，靠前的操作具有较高的优先级。每种操作都由一个空格隔开。

Output

　　只需输出一个数，这个数表示移动的次数。

Sample Input

　　3
　　AB BC CA BA CB AC

Sample Output

HINT

　　1≤n≤30，保证答案不会超过10^18。

Solution

　　先来说说DP（实际上是递推）的做法。

　　由于操作序列的优先级是固定的，那么对于每种操作序列，它的移动自始至终都是唯一的。所以我们称之为递推。

　　Hanoi问题还有一个经典性质就是，它的整个过程是可以用递归实现的。

　　用f[i][j]表示前i小的盘子现在全部堆叠在第j座塔上，把这i个盘子全部移到另一座塔上需要的步数。

　　不管这i个盘子下面还有没有盘子，f[i][j]是固定的（显然很好证明）。这就可以看出这个问题有很好的子任务性。

　　所以我们依然以上面提到的f[i][j]设计状态，顺便记录g[i][j]为这i个盘子从第j座塔移到了哪一座塔。

　　接着就可以愉快地考虑转移了：

　　首先操作序列是固定的，f[1][j]和g[1][j]都可以确定。

　　当i>1时，我们分类讨论一下。

　　先把i-1个盘子从j用f[i-1][j]的步数移到g[i-1][j]，然后第i个盘子就只能够移到剩下的那座塔，设这座塔为k。

　　然后要做的事是把位于g[i-1][j]的i-1个盘子移到k上。

　　　　如果g[i-1][g[i-1][j]]=k，那么万事大吉，直接花费f[i-1][g[i-1][j]]的步数完成转移；

　　　　如果g[i-1][g[i-1][j]]≠k，那么它只能等于j，无奈之下先把这i-1个盘子先移到j，

　　　　然后第i个盘子又只能够从k移到g[i-1][j]，由于g[i-1][j]=g[i-1][j]，这下可以放心地把这i-1个盘子放到第i个盘子上了。

　　总的转移方程为：

　　　　。

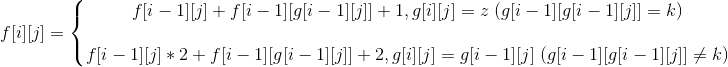　　然而小C刚开始做这题的的时候是没啥头绪的，所以开始打表找规律。

　　打表之前，有一个显而易见的结论：

　　每次移动的起点总是确定的，而终点可能确定也可能不确定。

　　就拿n=3，“AB BC CB AC BA CA”为例：

　　第一步，起点只能为“A”，终点可以是“B”、“C”，因为“AB”在“AC”前面，所以从把盘子从“A”挪到“B”→{2,3}{1}{}；

　　第二步，起点只能为“A”，终点只能为“C”→{3}{1}{2}；

　　第三步，起点只能为“B”，终点可以是“A”、“C”，“BC”在“BA”前面→{3}{}{1,2}；

　　第四步，起点只能为“A”，终点只能为“B”→{}{3}{1,2}；

　　第五步，起点只能为“C”，终点只能为“A”、“B”，“CB”在“CA”前面→{}{1,3}{2}……

　　注意第五步本来的最优走法是“CA”，而走“CB”导致最终步数为9而不是7。

　　所以能够影响答案的只有“AB”与“AC”之间，“BA”与“BC”之间，“CA”与“CB”之间的相对位置关系。

　　又由于“B”和“C”本质上是相同的，“AB”和“AC”本质上也是相同的，所以当n确定时，答案不会超过4种。

　　实际上，小C打表出来的答案只有3种。而且这3种的步数还分别是关于n的一阶递推式！

　　结论如下：f[1]=1，假设“AX”在“AY”前面。

　　　　若“XA”在“XY”前面，递推式为f[x]=f[x-1]*3+2；

　　　　若“XY”在“XA”前面且“YX”在“YA”前面，递推式为f[x]=f[x-1]*3；

　　　　若“XY”在“XA”前面且“YA”在“YX”前面，递推式为f[x]=f[x-1]*2+1。

　　小C也只能推导到这了，至于为什么是递推式，网络上其他题解也有证明。

　　但至于为什么是这几个递推式，就有待研究了，小C也不会证明，读者如有想法可以发表评论或是联系小C。

　　DP法：

#include <cstdio>

#include <cstring>

#include <algorithm>

#define MN 35

#define ll long long

using namespace std;

char c[];

ll f[MN][];

int g[MN][];

int n;

inline int read()

{

    int n=,f=; char c=getchar();

    while (c<'' || c>'') {if(c=='-')f=-; c=getchar();}

    while (c>='' && c<='') {n=n*+c-''; c=getchar();}

    return n*f;

}

int main()

{

    register int i,x,y,z;

    n=read();

    for (i=;i<=;++i)

    {

        scanf("%s",c);

        if (!g[][c[]-'A'+]) g[][c[]-'A'+]=c[]-'A'+;

    }

    f[][]=f[][]=f[][]=;

    for (i=;i<=n;++i)

        for (x=;x<=;++x)

        {

            y=g[i-][x]; z=-x-y;

            if (g[i-][y]==z) f[i][x]=f[i-][x]+f[i-][y]+,g[i][x]=z;

            else f[i][x]=f[i-][x]*+f[i-][y]+,g[i][x]=y;

        }

    printf("%lld",f[n][]);

}

　　观察找规律法：

#include <cstdio>

#include <cstring>

#include <algorithm>

#define ll long long

using namespace std;

ll ans;

int n,mov[];

char a[][];

inline int read()

{

    int n=,f=; char c=getchar();

    while (c<'' || c>'') {if(c=='-')f=-; c=getchar();}

    while (c>='' && c<='') {n=n*+c-''; c=getchar();}

    return n*f;

}

int main()

{

    register int i;

    n=read();

    for (i=;i<;++i) scanf("%s",a[i]);

    for (i=;i>=;--i) mov[a[i][]-'A']=a[i][]-'A';

    ans=;

    if (mov[mov[]]==) {for (i=;i<=n;++i) ans=ans*+;}

    else if (mov[mov[mov[]]]==mov[]) {for (i=;i<=n;++i) ans=ans*;}

    else {for (i=;i<=n;++i) ans=ans*+;}

    printf("%lld",ans);

}

Last Word

　　有一次通过自己瞎搞找出规律的经历还是很赛艇的。

　　题目中操作的720种排列方式明摆着就在告诉你，来打表找规律吧~

　　不过递推的方法也算让小C知道了Hanoi的一个经典性质。