machine learning 之 logistic regression

整理自Adrew Ng 的 machine learning课程week3

目录：

• 二分类问题
  • 模型表示
  • decision boundary
• 损失函数
• 多分类问题
• 过拟合问题和正则化
  • 什么是过拟合
  • 如何解决过拟合
  • 正则化方法

1、二分类问题

什么是二分类问题？

• 垃圾邮件 / 非垃圾邮件？
• 诈骗网站 / 非诈骗网站？
• 恶性肿瘤 / 非恶性肿瘤？

用表达式来表示：$y\in\left \{ 0,1 \right \}$，

\begin{Bmatrix}
0& : & nagetive & class\\
1& : & positive & class
\end{Bmatrix}

可以用线性回归处理分类问题吗？

当用线性回归处理分类问题时，可以选取一个阈值，如图所示，比如说，当$h_\theta(x) \geq \theta^Tx$，就预测$y=1$；当$h_\theta(x) < \theta^Tx$，就预测$y=0$；

当样本只有上下的8个红色叉叉时，玫红色的直线是线性回归的结果，当选取阈值为0.5时，根据玫红色的竖线，可以将正类和负类分开，没有问题；

但是，当添加一个样本，如图中的绿色叉叉，回归线就变成了绿色的直线，这时选取0.5为阈值时，会把上面的4个红色叉叉（正类）分到负类里面去，问题很大了；

此外，在二分类问题中，y=0或者y=1，而在线性回归中，$h_\theta(x)$可以大于1，也可以小于0，这也不合理；（在逻辑回归中$0<h_\theta(x)<1$）;

通过上面的例子得出结论，用线性回归做分类问题是不合理的，结果不稳定。

logistic regression模型的表示

不用线性回归模型，用逻辑回归模型：

$g(z)=\frac{1}{1+e^{-z}}$；$0<g(z)<1$。sigmoid函数 / logistic函数，函数图像如下：

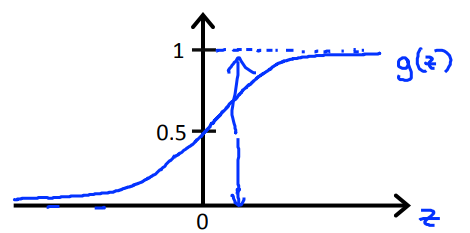
$h_\theta(x)=\frac{1}{1+e^{-\theta^Tx}}$

说明：$h_\theta(x)=P(y=1|x;\theta)$，代表估计y=1的概率；（Probability that y=1, given x, parameterized by $\theta$）

线性的Decision Boundary

将两个类分开的边界，如下图，design boundary就是$x_1+x_2=3$；

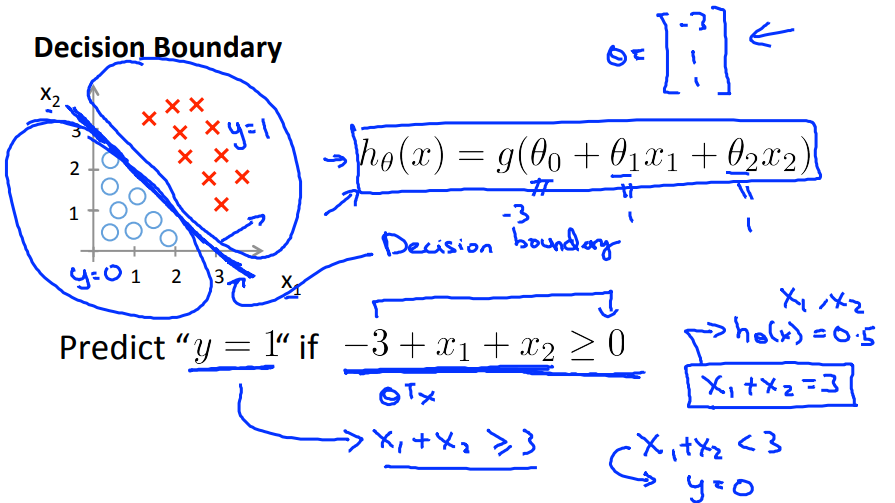
非线性的decision boundary

以下边界为，$x_1^2+x_2^2=1$

注意到，边界是在参数确定的时候才能画出来的，它是对应着指定的参数的。

2、损失函数

如何去求模型的参数呢？

如果考虑线性回归的情况，损失函数为平方损失，对于线性回归中的简单函数，这样子定义的损失函数是个凸函数，易求解；但是在逻辑回归中，模型是个复杂的非线性函数（$g(z)=\frac{1}{1+e^{-z}}$），平方损失下的损失函数不是个凸函数，有非常多的local minimal，不好求解；所以对逻辑回归，需要换个损失函数。

逻辑回归损失函数

$$cost(h_\theta(x),y)=\left\{\begin{matrix}
-log(h_\theta(x)) & if \; y=1 \\
-log(1-h_\theta(x)) & if \; y=0
\end{matrix}\right.$$

当y=1时，函数图像如左图所示，当$h_\theta(x)=1$时，cost=0；当$h_\theta(x)=0$时，cost趋向于无穷大；符合逻辑；

当y=0时，函数图像如右图所示，当$h_\theta(x)=0$时，cost=0；当$h_\theta(x)=1$时，cost趋向于无穷大；符合逻辑；

                 

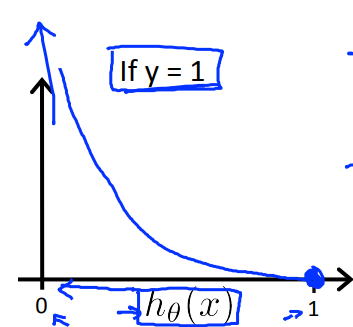
最重要的是，这个函数是凸的！

简化的损失函数和梯度下降

$cost(h_\theta(x),y)=-ylog(h_\theta(x))-(1-y)log(1-h_\theta(x))$

逻辑回归的损失函数基本上用的都是这个，为什么用这个函数？

• 可用极大似然估计求参数
• 凸函数
• 和上面的损失函数是等价的

故：

$J(\theta)=-\frac{1}{m}[\sum_{i=1}^m y^{(i)}logh_\theta(x^{(i)}) + (1-y^{(i)})log(1-h_\theta(x{(i)}))]$

求参$\theta$：$\underset{\theta}{min}J(\theta)$

给定x，预测y：$h_\theta(x)=\frac{1}{1+e^{-\theta^Tx}}$

梯度下降

$\theta_j=\theta_j-\alpha \frac{\partial J(\theta)}{\partial \theta_j}=\theta_j - \alpha \sum_{i=1}^m (h_\theta(x^{(i)})-y^{(i)}) x_j^{(i)} $

这里的参数更新形式和线性回归中是一样的，但是注意到$h_\theta(x)$是不一样的；

注意在逻辑分类模型中，feature scaling也是有用的；

高级优化方法

除了梯度下降算法，还有一些更加高级的、老练的、速度更快的优化方法：“Conjudge gradient、BFGS、L-BFGS”

3、多分类问题

邮件分类：朋友、家人、工作.......

天气：晴、多云、雨、雪.......

所分类问题的一个思路是：one-vs-all；

如下，对于有3类的多分类问题，构造3个分类函数，每次只把一个类和其他的类区别开来，$h_\theta^{(i)}(x)；i=1,2,3$：

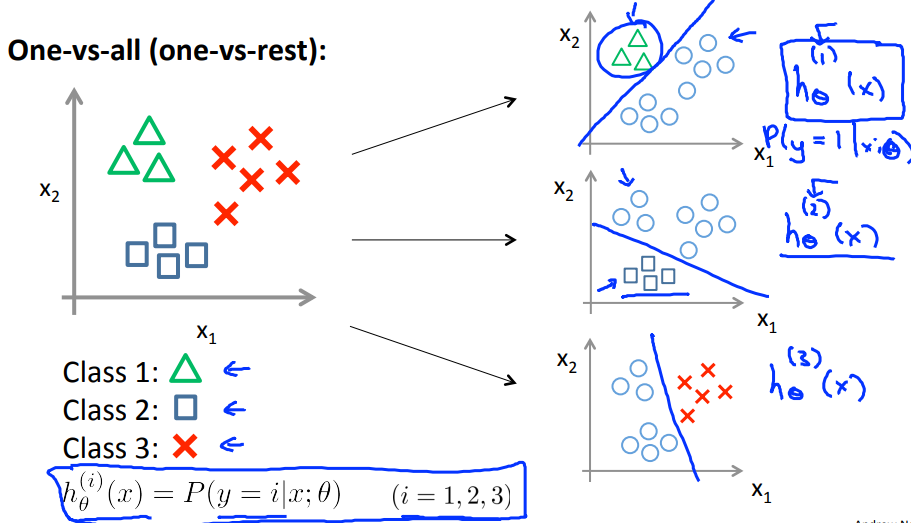
因此，每一个分类器都可以得到一个$y=i(i=1,2,3)$的概率，最大的概率的i就是类别结果，即预测为：$ \underset {i}{max} h_\theta^{(i)}(x)；i=1,2,3$

4、过拟合问题和正则化

过拟合问题

如图所示，对于房价预测问题，有三个模型：

第一个模型很简单，拟合的不是很好，可以称之为“欠拟合”，有比较大的偏差（bias）；

第二个模型比第一个模型复杂一点，拟合的不错，可以认为“拟合的刚刚好”；

第三个模型非常复杂，拟合的天衣无缝，可以称之为“过拟合”，又比较大的方差（variance）；

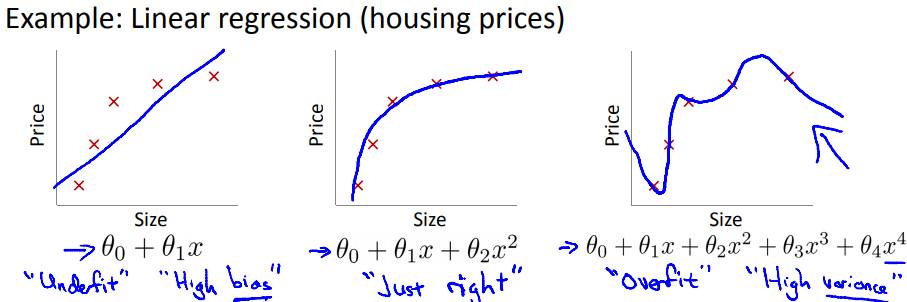
过拟合说的就是第三幅图中的的问题，如果我们有很多的features，学习得到的模型可以对训练数据拟合的非常好（$J(\theta) \approx 0$），但是在拟合新的数据的时候却做的不好，泛化能力弱；

类似的，在逻辑回归中：

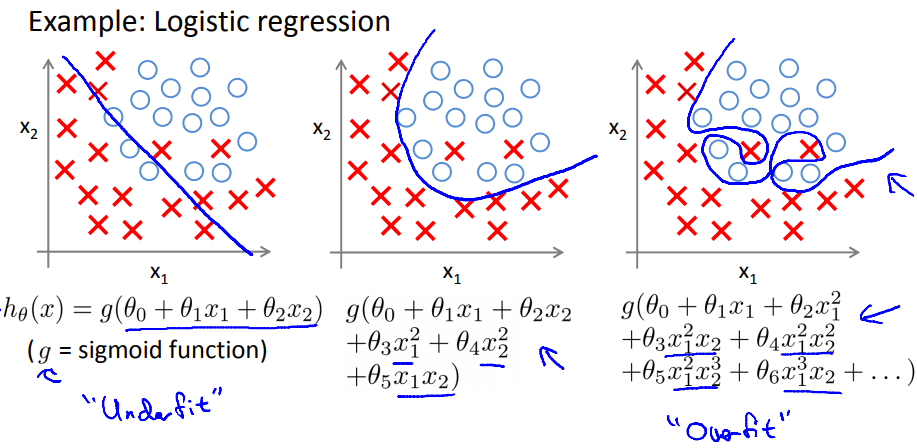
如何解决过拟合问题？

• 减少feature的数目
  • 可以手动的选择保留哪些feature
  • 一些自动的模型选择算法（model selection algorithm）
• 正则化
  • 保留所有的feature，但是reduce magnitude/values of parameters
  • 当有很多的feature，每个都对预测有点贡献的时候，非常有用

正则化后的损失函数

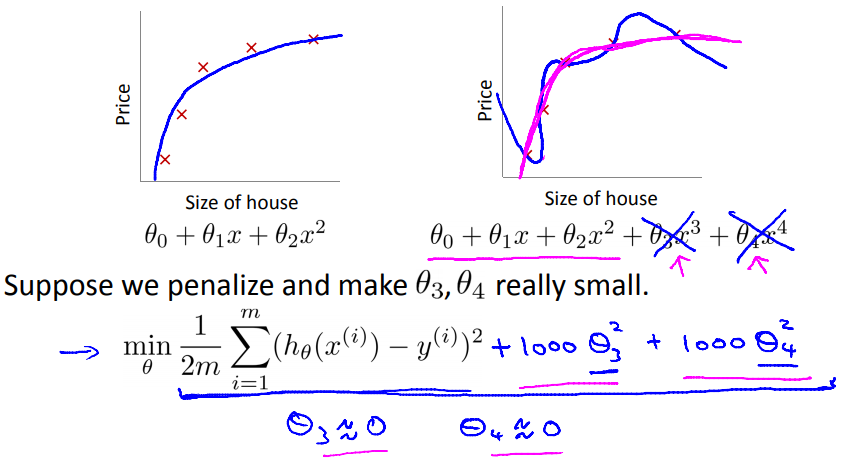
如下图所示，逻辑上，当在原本的损失函数后加惩罚项的话，$\theta_3$和$\theta_4$就会变得十分的小，这样虽然模型复杂，但是高阶的部分其实非常小，就类似于低阶的函数；

正则化“简化”了模型，使得模型过拟合的倾向减小；

正则化线性回归：

$J(\theta)=\frac{1}{2m} [\sum_{i=1}^m (h_\theta(x^{(i)})-y^{(i)})^2 + \lambda \sum_{j=1}^n \theta_j^2]$

注意到，当$\lambda$非常大的时候，可以会出现欠拟合的情况；

此时的梯度下降算法的更新为：

$\theta_0=\theta_0-\alpha  \frac{1}{m} (h_\theta(x^{(i)})-y^{(i)})x_0^{(i)} $

$\theta_j=\theta_j-\alpha [ \frac{1}{m} (h_\theta(x^{(i)})-y^{(i)})x_j^{(i)} + \frac{\lambda}{m}\theta_j] $；j=1,2,.....n；

注意：$\theta_0$是不更新的

注意到：

$\theta_j=\theta_j(1 - \alpha\frac{\lambda}{m}) - \alpha \frac{1}{m} (h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}  $

$1 - \alpha\frac{\lambda}{m}$是个极其接近1的数字，可能是0.99，所以正则化后的更新策略和之前的对比，就是让$\theta_j$更小了一些；

Normal Equation

$$\theta=(x^Tx+\lambda\begin{bmatrix}
0 & & &\\ 
& 1 & & \\
& & 1 & \\
& & &...
\end{bmatrix}))^{-1}x^Ty$$

在无正则化的线性回归问题中，Normal Equation存在一个不可逆的问题，但是可以证明$(x^Tx+\lambda\begin{bmatrix}
0 & & &\\ 
& 1 & & \\
& & 1 & \\
& & &...
\end{bmatrix}))$是可逆的；

正则化的logistic regression

与线性回归的正则化一样，只要把模型函数（$h_\theta(x)$）换了即可