CF385C Bear and Prime Numbers 数学

题意翻译

给你一串数列a.对于一个质数p,定义函数f(p)=a数列中能被p整除的数的个数.给出m组询问l,r,询问[l,r]区间内所有素数p的f(p)之和.

题目描述

Recently, the bear started studying data structures and faced the following problem.

You are given a sequence of integers x1,x2,...,xn x_{1},x_{2},...,x_{n} x1​,x2​,...,xn​ of length n n n and m m m queries, each of them is characterized by two integers li,ri l_{i},r_{i} li​,ri​ . Let's introduce f(p) f(p) f(p) to represent the number of such indexes k k k , that xk x_{k} xk​ is divisible by p p p . The answer to the query li,ri l_{i},r_{i} li​,ri​ is the sum: 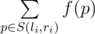, where S(li,ri) S(l_{i},r_{i}) S(li​,ri​) is a set of prime numbers from segment [li,ri] [l_{i},r_{i}] [li​,ri​] (both borders are included in the segment).

Help the bear cope with the problem.

输入输出格式

输入格式：

The first line contains integer n n n (1<=n<=106) (1<=n<=10^{6}) (1<=n<=106) . The second line contains n n n integers x1,x2,...,xn x_{1},x_{2},...,x_{n} x1​,x2​,...,xn​ (2<=xi<=107) (2<=x_{i}<=10^{7}) (2<=xi​<=107) . The numbers are not necessarily distinct.

The third line contains integer m m m (1<=m<=50000) (1<=m<=50000) (1<=m<=50000) . Each of the following m m m lines contains a pair of space-separated integers, li l_{i} li​ and ri r_{i} ri​ (2<=li<=ri<=2⋅109) (2<=l_{i}<=r_{i}<=2·10^{9}) (2<=li​<=ri​<=2⋅109) — the numbers that characterize the current query.

输出格式：

Print m m m integers — the answers to the queries on the order the queries appear in the input.

输入输出样例

输入样例#1：
复制

6
5 5 7 10 14 15
3
2 11
3 12
4 4

输出样例#1： 复制

9
7
0

输入样例#2： 复制

7
2 3 5 7 11 4 8
2
8 10
2 123

输出样例#2： 复制

0
7

首先可以线性筛筛出 1e7 里面所有的素数；
对于每一个x[i] ，我们记录其次数，然后类似于埃筛的做法，对于每个素数，用 sum [ i ] 来累计有该素数因子的数的个数；
最后用前缀和维护；

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstdlib>
#include<cstring>
#include<string>
#include<cmath>
#include<map>
#include<set>
#include<vector>
#include<queue>
#include<bitset>
#include<ctime>
#include<deque>
#include<stack>
#include<functional>
#include<sstream>
//#include<cctype>
//#pragma GCC optimize("O3")
using namespace std;
#define maxn 10000005
#define inf 0x3f3f3f3f
#define INF 9999999999
#define rdint(x) scanf("%d",&x)
#define rdllt(x) scanf("%lld",&x)
#define rdult(x) scanf("%lu",&x)
#define rdlf(x) scanf("%lf",&x)
#define rdstr(x) scanf("%s",x)
typedef long long  ll;
typedef unsigned long long ull;
typedef unsigned int U;
#define ms(x) memset((x),0,sizeof(x))
const long long int mod = 1e9 + 7;
#define Mod 1000000000
#define sq(x) (x)*(x)
#define eps 1e-3
typedef pair<int, int> pii;
#define pi acos(-1.0)
const int N = 1005;
#define REP(i,n) for(int i=0;i<(n);i++)
typedef pair<int, int> pii;
inline ll rd() {
	ll x = 0;
	char c = getchar();
	bool f = false;
	while (!isdigit(c)) {
		if (c == '-') f = true;
		c = getchar();
	}
	while (isdigit(c)) {
		x = (x << 1) + (x << 3) + (c ^ 48);
		c = getchar();
	}
	return f ? -x : x;
}

ll gcd(ll a, ll b) {
	return b == 0 ? a : gcd(b, a%b);
}
ll sqr(ll x) { return x * x; }

/*ll ans;
ll exgcd(ll a, ll b, ll &x, ll &y) {
	if (!b) {
		x = 1; y = 0; return a;
	}
	ans = exgcd(b, a%b, x, y);
	ll t = x; x = y; y = t - a / b * y;
	return ans;
}
*/

ll qpow(ll a, ll b, ll c) {
	ll ans = 1;
	a = a % c;
	while (b) {
		if (b % 2)ans = ans * a%c;
		b /= 2; a = a * a%c;
	}
	return ans;
}

int n;
int x[maxn];
int m;
int cnt[maxn];
int prime[maxn];
int tot = 0;
int sum[maxn];
bool vis[maxn];

void init() {
	vis[1] = 1;
	for (int i = 2; i < maxn; i++) {
		if (!vis[i])prime[++tot] = i;
		for (int j = 1; prime[j] * i < maxn; j++) {
			vis[prime[j] * i] = 1;
			if (i%prime[j] == 0)break;
		}
	}
}

int main()
{
	//ios::sync_with_stdio(0);
	rdint(n);
	for (int i = 1; i <= n; i++)rdint(x[i]), cnt[x[i]]++;
	init();
	for (int i = 1; i <= tot; i++) {
		for (int j = 1; j*prime[i] < maxn; j++) {
			sum[i] += cnt[j*prime[i]];
		}
	}
	for (int i = 1; i <= tot; i++)sum[i] += sum[i - 1];
	rdint(m);
	while (m--) {
		int l, r; rdint(l); rdint(r);
		int pos1 = upper_bound(prime + 1, prime + 1 + tot, r) - prime - 1;
		int pos2 = lower_bound(prime + 1, prime + 1 + tot, l) - prime - 1;
//		cout << pos1 << ' ' << pos2 << endl;
		cout << sum[pos1] - sum[pos2] << endl;
	}
    return 0;
}