牛客网多校训练第一场 A - Monotonic Matrix（Lindström–Gessel–Viennot lemma）

链接：

https://www.nowcoder.com/acm/contest/139/A

题意：

求满足以下条件的n*m矩阵A的数量模(1e9+7)：
A(i,j) ∈ {0,1,2}, 1≤i≤n, 1≤j≤m.
A(i,j) ≤ A(i+1,j), 1≤i<n, 1≤j≤m.
A(i,j) ≤ A(i,j+1), 1≤i≤n, 1≤j<m.
其中1 ≤ n,m ≤ 1e3。

分析：

考虑01和12的分界线，
是(n,0)到(0,m)的两条不相交（可重合）路径。
平移其中一条变成(n+1,1)到(1,m+1)，
变成(n,0)到(0,m)、(n+1,1)到(1,m+1)的严格不相交路径。
套Lindström–Gessel–Viennot lemma，
答案是C(n+m,n) * C(n+m,n) - C(n+m,n+1) * C(n+m,n-1)。

Lindström–Gessel–Viennot lemma简介：

求a1到b1, a2到b2, ..., an到bn的严格不相交路径种数。

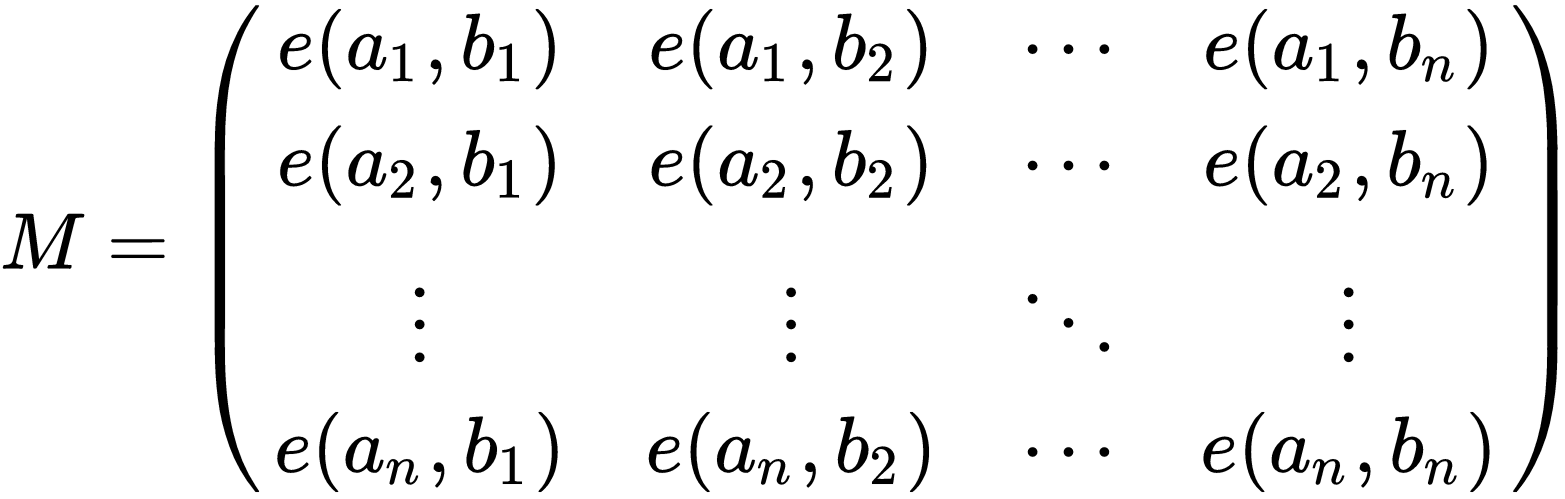
计算以上矩阵的行列式即可，其中e(a,b)是从a到b的方法数。

代码：

 #include <cstdio>

 typedef long long int LLI;
 const int UP =  *  + ;
 const LLI MOD = 1e9 + ;
 LLI f[UP]; // 阶乘

 LLI qmod(LLI x, LLI n, LLI mod) { // 快速幂模
     x %= mod;
     LLI res = ;
     while(n) {
         if(n & ) res = res * x % mod;
         n >>= ;
         x = x * x % mod;
     }
     return res;
 }

 LLI inv(LLI a, LLI mod) { // 逆元
     return qmod(a, mod-, mod);
 }

 void constant() { // 预处理阶乘
     f[] = ;
     for(int i = ; i < UP; i++) f[i] = f[i-] * i % MOD;
 }

 LLI C(int n, int m) { // 组合数，从n个里取m个
     return f[n] * inv(f[m]*f[n-m], MOD) % MOD;
 }

 int main() {
     constant();
     int n, m;
     while(~scanf("%d%d", &n, &m)) {
         LLI ans = (C(n+m,n) * C(n+m,n) - C(n+m,n+) * C(n+m,n-) % MOD + MOD) % MOD;
         printf("%lld\n", ans);
     }
     return ;
 }