【枚举约数】Gym - 101412A - Ginkgo Numbers

给你一堆定义，问你在那个定义下，<p,q>是不是素数。其实那堆定义都不用管，只要看最下面给你的提示即可。

根据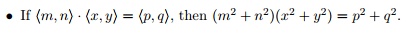，只要把m^2+n^2当一个整体，去枚举(p^2+q^2）的约数即可，然后再枚举m，

这样的枚举出来是必要的，然后再根据这个充要条件判一下即可。

#include<cstdio>
#include<cmath>
using namespace std;
const double EPS=0.00000001;
int T;
int p,q;
bool check(int i){
	for(int M=1;M*M<=i;++M){
		int N=(int)(sqrt(i-M*M)+0.5);
		if(fabs(sqrt(i-M*M)-(double)N)<EPS){
			if((M*p+N*q)%(M*M+N*N)==0 && (M*q-N*p)%(M*M+N*N)==0){
				return 0;
			}
		}
	}
	return 1;
}
int main(){
	scanf("%d",&T);
	for(;T;--T){
		scanf("%d%d",&p,&q);
		int ppqq=p*p+q*q;
		for(int i=2;i*i<=ppqq;++i){
			if(ppqq%i==0){
				if(i*i!=ppqq){
					if(!check(i)){
						puts("C");
						goto OUT;
					}
				}
				else{
					if(!check(i) || !check(ppqq/i)){
						puts("C");
						goto OUT;
					}
				}
			}
		}
		puts("P");
		OUT:;
	}
	return 0;
}