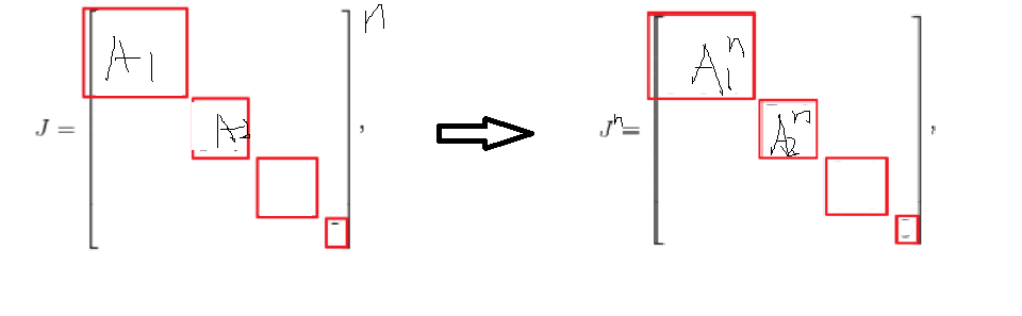
2019清明期间qbxt培训qaq

4.4下午：矩阵qwq

• part1矩阵乘法：
• 概念：

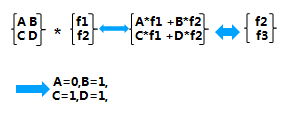
一个m×p的矩阵A 乘 一个p×n的矩阵B 得到一个矩阵一个m×n的矩阵AB

其中：

矩阵乘法满足结合律、分配率，不满足交换律

矩阵乘法—solution：

struct m{
    int a[][];
};
m operator *(m a,m b){
    m c;
    for(int i=;i<=;i++)
        for(int j=;j<=;j++){
            c.a[i][j]=;
            for(int k=;k<=;k++)
    c.a[i][j]=(c.a[i][j]+a.a[i][k]*b.a[k][j])%p;
        }return c;}

eg1：斐波那契数列

【题目背景】

yy最近在数学课上学了斐波那契数列，已知斐波那契数列满足f（n）=f（n-1）+f（n-2）且f(1)=f(2)=1，现在yy的老师想要考考他们，老师随意给出一个数k，要大家一个个的回答他斐波那契数列的第k项，下一个就轮到yy了，但 yy做了半天，怎么也想不到做法，请你写一个程序帮助yy快速的算出第k项。

【输入格式】

输入只有一行，为这个数k。

【输出格式】

只有一行，输出斐波那契数列的第k项（取模1e9+7）

【输入样例】      【输出样例】

15                            610

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
long long p=;
int k;
struct m{
    int a[][];
};
m operator *(m a,m b)//矩阵乘法的标程qwq
{
    m c;
    for(int i=;i<=;i++)
        for(int j=;j<=;j++){
            c.a[i][j]=;//先把全部的值都赋为0 
            for(int k=;k<=;k++)
                c.a[i][j]=(c.a[i][j]+a.a[i][k]*b.a[k][j])%p;

//eg： 1.c.a[0][0]=(c.a[0][0]+a.a[0][0]*b.a[0][0])%pp;
// 2.c.a[0][0]=(c.a[0][0]+a.a[0][1]*b.a[1][0])%pp;
//综上：c.a[0][0]=(a.a[0][1]*b.a[1][0]+a.a[0][0]*b.a[0][0])%pp;

        }
        return c;
}
int main()
{
    cin>>k;
    m a;
    a.a[][]=;a.a[][]=;
    a.a[][]=;a.a[][]=;
    m ans;
    ans.a[][]=;ans.a[][]=;
    ans.a[][]=;ans.a[][]=;//单位矩阵，当一来用； 
    int b=k-;
    while(b){//结构体乘法 利用快速幂思想 
        if(b&)ans=ans*a;
        a=a*a;
        b/=;
    }
    int fk=(ans.a[][]+ans.a[][])%p;//ans.a[0][0]*f(1)+ ans.a[0][1]*f(2)
    cout<<fk<<endl;
}

思路：构建转移矩阵：

---

eg2：

【题目背景】

yy今天又上数学课了，这次老师又问了yy一个新问题：

计算f(n) = 4f(n-1) – 3f(n-2) + 2f(n-4) 的第k项，老师会给定这个数列的前四项，以及一个数k，老师说如果yy可以解出来就以yy的名字命名这个数列，yy很想有一个以他名字命名的数列，请你帮帮他。

【输入格式】

第一行：四个数，分别为这个数列的第1,2,3,4项；

第二行：一个数k表示要求的是这个数列的第几项。

【输出格式】

一个数，为这个数列的第k项

【输入样例】       【输出样例】

1 1 3 5            3711（不对请指正）

10

struct along{
    int a[][];
};
along operator *(along a,along b)
{
    along c;
    for(int i=;i<=;i++){

      for(int j=;j<=;j++){
          c.a[i][j]=;
          for(int k=;k<=;k++)
          c.a [i][j]=(c.a[i][j]+a.a[i][k]*b.a[k][j])%p;
      }
}
      return c;
}
int main()
{
    int x,y,z,w,k;
    cin>>x>>y>>z>>w;
    cin>>k;
    int b=k-;
    along a;
    a.a[][]=;a.a[][]=;a.a[][]=;a.a[][]=;
    a.a[][]=;a.a[][]=;a.a[][]=;a.a[][]=;
    a.a[][]=;a.a[][]=;a.a[][]=;a.a[][]=;
    a.a[][]=;a.a[][]=;a.a[][]=-;a.a[][]=;//转移矩阵
    along ans;
    ans.a[][]=;ans.a[][]=;ans.a[][]=;ans.a[][]=;
    ans.a[][]=;ans.a[][]=;ans.a[][]=;ans.a[][]=;
    ans.a[][]=;ans.a[][]=;ans.a[][]=;ans.a[][]=;
    ans.a[][]=;ans.a[][]=;ans.a[][]=;ans.a[][]=;//单位矩阵
    while(b){
        if(b&)ans=ans*a;
        a=a*a;
        b/=;
    }
    int fk=(ans.a[][]*x+ans.a[][]*y+ans.a[][]*z+ans.a[][]*w)%p;
    cout<<fk<<endl;
}//include什么的自己加吧qwq

（为什么我u盘老是丢东西啊啊啊恐惧哪天培训的东西丢光了（Dev一改代码就丢啊啊啊）自闭）

我滴思路？？

1.自己搞一搞，搞出转移矩阵(至于怎么搞，可以参见eg1

ps：之前一直搞不懂的一点，就是这个奇奇怪怪的式子乘转移矩阵的k-1次方是怎么搞到的fk，后来发现fk就是那个奇奇怪怪的式子啊qwq（大概没讲明白）

2.写代码(打表一时爽)

eg3：（poj3233）

【题目背景】

yy看中了nili千古神犇zay的一包金色袋子的零食，yy决定为难一下zay，于是yy问了azy一道题：给定一个n*n的矩阵A，求A + A^2 + A^3 + … + A^k的结果。zay居然不会qwq！显然zay不能在yy面前chuchou，现在请你帮帮zay，使他快速的算出来，如果算不出来，zay的零食就是yy的了qwq

（不想写了qwqqwqqwq求助sy去了qwq什么时候更代码随缘吧qwq）

eg4：

【题目背景】

sy要去狼外婆家买markdown（尽管我也不知道为啥qwq）现在给定一个有向图，问从sy所在地恰好走k步（允许重复经过边）到达狼外婆家的最短路长度。 有向图点数<=50 k<=10^9

原题来源于hdu

【输入格式】

输入数据有多组, 每组的第一行是2个整数 n, m(0 < n <= 20, m <= 100) 表示地图上共有n个点, 为了方便起见, 点从0到n-1编号,接着有m行, 每行有两个整数 s, t (0<=s,t<n) 表示从s点能到t点, 注意图是有向的.接着的一行是两个整数T,表示有T组询问(1<=T<=100),
接下来的T行, 每行有三个整数 A, B, k, 表示问你从A 点到 B点恰好经过k个点的方案数 (k < 20), 可以走重复边。如果不存在这样的走法, 则输出0
当n, m都为0的时候输入结束

【输出格式】

计算每次询问的方案数, 由于走法很多, 输出其对1000取模的结果

【输入样例】

4 4

0 1

0 2

1 3

2 3

2

0 3 2

0 3 3

3 6

0 1

1 0

0 2

2 0

1 2

2 1

2

1 2 1

0 1 3

0 0

【输出样例】

2

0

1

3

solution：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <string.h>
#include <vector>
#include <queue>    //hdu2157
#define mod 1000
using namespace std;
int n;
struct matrix
{
    int a[][];
    void init(){
        for(int j=; j<; ++j){
            for(int t=; t<; ++t)
                a[j][t]=;
        }
    }
}p;

matrix mul(matrix a1, matrix b1)
{
    matrix q;
    q.init();
    int t, j, k;
    for(j=; j<n; ++j){
        for(t=; t<n; ++t){
            for(k=; k<n; ++k){
                q.a[j][t]+=a1.a[j][k]*b1.a[k][t];
                q.a[j][t]%=mod;
            }
        }
    }
    return q;
}
matrix f(int x)
{
    matrix q, s=p;
    int t, j;
    for(j=; j<n; ++j){    //构建单位矩阵
        for(t=; t<n; ++t){
            if(j==t)
                q.a[j][t]=;
            else q.a[j][t]=;
        }
    }
    while(x){
        if(x&)
            q=mul(s, q);
        x=x>>;
        s=mul(s, s);
    }
    return q;
}

int main()
{
    int m ,t, T, s, k, s1, s2, g;
    while(scanf("%d%d", &n, &m)!=EOF){
        if(n==&&m==)break;
        p.init();
        for(t=; t<m; ++t){
            scanf("%d%d", &s, &g);
            p.a[s][g]=;    //有向的
        }
        scanf("%d", &T);
        while(T--){
            scanf("%d%d%d", &s1, &s2, &k);
            matrix result=f(k);
            printf("%d\n", result.a[s1][s2]);  //s1到s2的路径总数
        }
    }
    return ;
}//假装是自己写的qwq

特殊矩阵的矩阵乘法qwq

• 上三角矩阵

• 上三角*上三角=上三角qwq

• 分块矩阵
• 分块*分块=分块
• 对角矩阵(对角线有数）
• 对称矩阵

• part2高斯消元 ：

原理不想讲辽，gc数学都说了，直接理解代码吧……

【题目背景】

某腾讯游戏最近新出了高斯消消乐，大佬wz想要去腾讯游戏应聘，现在公司要求写高斯消元的代码，请你帮帮他，帮他写一份代码吧qwq

【输入格式】

第一行：两个数，分别为m和n（其实他俩一样的qwq）

第2~m+1行：每行n+1个数，分别表示n个数和一个答案

【输出格式】

输出消元后的矩阵

【输入样例】       【输出样例】

没有输入样例        没有输出样例

只有求助解释check

上代码（from lh）（注释from lz）：

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<cstdlib>
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<int,int> pr;
const double pi=acos(-);
#define rep(i,a,n) for(int i=a;i<=n;i++)
#define per(i,n,a) for(int i=n;i>=a;i--)
#define Rep(i,u) for(int i=head[u];i;i=Next[i])
#define clr(a) memset(a,0,sizeof a)
#define pb push_back
#define mp make_pair
#define fi first
#define sc second
ld eps=1e-;
ll pp=;
ll mo(ll a,ll pp){if(a>= && a<pp)return a;a%=pp;if(a<)a+=pp;return a;}
ll powmod(ll a,ll b,ll pp){ll ans=;for(;b;b>>=,a=mo(a*a,pp))if(b&)ans=mo(ans*a,pp);return ans;}
ll read(){
    ll ans=;
    char last=' ',ch=getchar();
    while(ch<'' || ch>'')last=ch,ch=getchar();
    while(ch>='' && ch<='')ans=ans*+ch-'',ch=getchar();
    if(last=='-')ans=-ans;
    return ans;
}
//head（lh的代码头）
int n,m;
double a[][];

bool check(int k){
    if(fabs(a[k][n+])<eps)return ;// 如果小于0，返回1
    for(int i=;i<=n;i++)
        if(fabs(a[k][i])>eps)return ;//第k行的每个数都大于0
    return ;
}
int main(){
    n=read();m=read();//m*n的矩阵，
    // a_i,1 a_i,2 ... a_i,n a_i,n+1
    for(int i=;i<=m;i++)
        for(int j=;j<=n+;j++)a[i][j]=read();//输入矩阵元素(因为除了这个m*n的矩阵，还要有一行答案qwq） （看洛谷题吧qwq）
    for(int j=;j<=m;j++){
            for(int k=;k<=n+;k++)cout<<a[j][k]<<" ";
            puts("");
        }//先把矩阵输出辽一遍
    int flag=;
    for(int i=;i<=n;i++){
        int t=i;
        while(a[t][i]== && t<=n)t+=;
        if(t==n+){
            flag=;
            continue;
        }//if判断是否有一行全为0，如果全为0 那么我们就少了至少1个方程，那么这个方程显然无唯一解
        for(int j=;j<=n+;j++)swap(a[i][j],a[t][j]);//交换第i行和第t行的值，目的在于交换第i行和第t行后可以使a[1][1]！=0
        double kk=a[i][i];//找到对角线qwq
        for(int j=;j<=n+;j++)a[i][j]/=kk;//把这一行的每一项都除以对角线，使得对角线为1
        for(int j=;j<=m;j++) //这里真的要详细地讲一讲咯
            if(i!=j){//首先i！=j这样就不再消对角线上的数了
                double kk=a[j][i];//定义kk为第j行第i列的数
                for(int k=;k<=n+;k++)//把每一项消成0qwq（先把第一列除了对角线全消为0然后第二第三……）
                // 关于处理对角线这里以i=1，j=3做例子：当k=3时，a[3][3]-=a[3][1]*a[1][3]而这个时候a[3][1]已经为0，故对对角线无影响
                    a[j][k]-=kk*a[i][k];
            }
        puts("------------");//画一个杠杠来分割每一次消元结果
        for(int j=;j<=m;j++){
            for(int k=;k<=n+;k++)cout<<a[j][k]<<" ";//输出每次消元结果
            puts("");//输出空格
        }
    }
    if(flag){//判断无解和多解的情况（上面已经提到了） 已经懵bi求救qwq
        for(int i=;i<=m;i++)
            if(!check(i)){//利用check判断是无解还是多解
                printf("No solution\n");
                return ;
            }
            //每个答案行如果有一个等于0的数就多解？？
        printf("So many solutions\n");
    }
}

东西又丢了！！！

补题：

来自洛谷高斯消元板子：

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<cstdlib>
using namespace std;
long long read(){
    long long ans=;
    char last=' ',ch=getchar();
    while(ch<'' || ch>'')last=ch,ch=getchar();
    while(ch>='' && ch<='')ans=ans*+ch-'',ch=getchar();
    if(last=='-')ans=-ans;
    return ans;
}
int n,m;
double a[][];

int main(){
    n=read();
    for(int i=;i<=n;i++)
        for(int j=;j<=n+;j++)a[i][j]=read();
    int flag=;
    for(int i=;i<=n;i++){
        int t=i;
        while(a[t][i]== && t<=n)t+=;
        if(t==n+){
            flag=;
            continue;
        }
        for(int j=;j<=n+;j++)swap(a[i][j],a[t][j]);
        double kk=a[i][i];
        for(int j=;j<=n+;j++)a[i][j]/=kk;
        for(int j=;j<=n;j++)
            if(i!=j){
                double kk=a[j][i];
                for(int k=;k<=n+;k++)
                    a[j][k]-=kk*a[i][k];
            }
        }
    if(flag)printf("No Solution\n");
    else {for(int i=;i<=n;i++)
         printf("%.2lf\n",a[i][n+]);}
         return ;
}
//和上面代码差不多的，只不过这个输出的是第n+1行，也就是每一个未知数的解（因为都消成1了qwq）

行列式-定义:

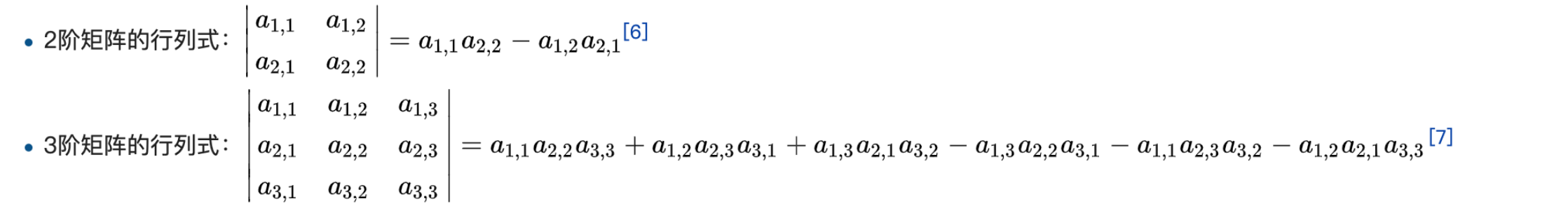
行列式计算：

1.利用高斯消元将原矩阵变为对角矩阵

2.将对角线上的值连乘得到行列式

3.同一行改变数值（数值和不变）行列式值不变

4.无解：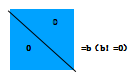

开始讲矩阵逆元了qwq：：：（某位不愿透漏姓名的许姓长贵一直在催的东西qwq）

先讲定义：

逆元的定义：若矩阵B*A=I （单位矩阵I）则称B为A的左逆元（同理右逆元也可以推算）

有逆元的前提： 矩阵行列式不为0

求矩阵逆元的方法：

如何求左逆元？B*A=I A =>I 同时<=>操作 I=>B(A的逆元）【对行进行高斯消元】

如何求右逆元？ A=>I

同时<=>操作 【对列进行高斯消元】

I=>B(A的逆元）

这个对行对列进行高斯消元没搞明白qwq？？？

看代码吧qwq（from钟神）：

【问题描述】

你是能看到第一题的 friends 呢。

——hja

众所周知，小葱同学擅长计算，尤其擅长计算组合数，但这个题和组合数没什么关系。

按照规矩，大家还是练习一下，这个矩阵求逆的模板题。

给你一个N× N的矩阵A，求A在模p意义下的逆矩阵B是多少。即你要找到一个矩阵B，使得AB模p得到的结果为单位矩阵，输出任意一种解即可。

【输入格式】

第一行两个整数N, mod。

接下来N行N个数代表矩阵。

【输出格式】

输出N行N个数代表逆矩阵，保证答案一定存在。

【样例输入】 

2 5

1 2

3 4

【样例输出】

3 1

4 2

【数据规模与约定】

对于10%的数据，N = 1。

对于40%的数据，N≤ 6。

对于另外20%的数据，p= 2。

对于100%的数据，1 ≤ N ≤ 100,2 ≤p≤ 10⁹并且p为一个质数，同时读入的矩阵内的数一定在[0, p − 1]，你输出的答案也需要保证这一点。

标程（不是钟神的，也不是我的qwq（懒得自己写了qwq））

#include<cstdio>
#include<iostream>
using namespace std;
typedef long long LL;
const int N=;
int mod;
int n,m;
LL f[N][N<<];//与下文相照应，这里N<<1指N/2，为了构造单位矩阵而乘的2
LL r,ret;
LL ksm(LL u,LL v){
ret=;
while(v){
if(v&)ret=ret*u%mod;
u=u*u%mod;v>>=;
}
return ret;
}
int main(){
scanf("%d%d",&n,&mod);m=n*; //乘2是为了后面建立一个单位矩阵
for(int i=;i<=n;++i){
for(int j=;j<=n;j++)scanf("%lld",&f[i][j]);//输入n*n的矩阵
f[i][n+i]=; //在 f后面又搞了一个单位矩阵qwq
}
for(int i=;i<=n;++i){ //高斯消元的板子
for(int j=i;j<=n;j++)
if(f[j][i]){
for(int k=;k<=m;k++)
swap(f[i][k],f[j][k]);
break;
}
if(!f[i][i]){puts("No Solution");return ;} //判断是否有解（对角线为0)
r=ksm(f[i][i],mod-);
for(int j=i;j<=m;++j)
f[i][j]=f[i][j]*r%mod;
for(int j=;j<=n;++j)
if(j!=i){
r=f[j][i];
for(int k=i;k<=m;++k)
f[j][k]=(f[j][k]-r*f[i][k]%mod+mod)%mod;
}
}
for(int i=;i<=n;++i,puts(""))
for(int j=n+;j<=m;++j)printf("%lld ",f[i][j]);
return ;
}

行我不想写了qwq

end-