第四百一十四节，python常用算法学习

本节内容

算法定义
时间复杂度
空间复杂度
常用算法实例

1.算法定义

算法（Algorithm）是指解题方案的准确而完整的描述，是一系列解决问题的清晰指令，算法代表着用系统的方法描述解决问题的策略机制。也就是说，能够对一定规范的输入，在有限时间内获得所要求的输出。如果一个算法有缺陷，或不适合于某个问题，执行这个算法将不会解决这个问题。不同的算法可能用不同的时间、空间或效率来完成同样的任务。一个算法的优劣可以用空间复杂度与时间复杂度来衡量。

一个算法应该具有以下七个重要的特征：

①有穷性（Finiteness）：算法的有穷性是指算法必须能在执行有限个步骤之后终止；

②确切性(Definiteness)：算法的每一步骤必须有确切的定义；

③输入项(Input)：一个算法有0个或多个输入，以刻画运算对象的初始情况，所谓0个输入是指算法本身定出了初始条件；

④输出项(Output)：一个算法有一个或多个输出，以反映对输入数据加工后的结果。没有输出的算法是毫无意义的；

⑤可行性(Effectiveness)：算法中执行的任何计算步骤都是可以被分解为基本的可执行的操作步，即每个计算步都可以在有限时间内完成（也称之为有效性）；

⑥高效性(High efficiency)：执行速度快，占用资源少；

⑦健壮性(Robustness)：对数据响应正确。

叫卖录音网
 录音网站

2. 时间复杂度

计算机科学中，算法的时间复杂度是一个函数，它定量描述了该算法的运行时间,时间复杂度常用大O符号（大O符号（Big O notation）是用于描述函数渐进行为的数学符号。更确切地说，它是用另一个（通常更简单的）函数来描述一个函数数量级的渐近上界。在数学中，它一般用来刻画被截断的无穷级数尤其是渐近级数的剩余项；在计算机科学中，它在分析算法复杂性的方面非常有用。）表述，使用这种方式时，时间复杂度可被称为是渐近的，它考察当输入值大小趋近无穷时的情况。

大O，简而言之可以认为它的含义是“order of”（大约是）。

无穷大渐近
大O符号在分析算法效率的时候非常有用。举个例子，解决一个规模为 n 的问题所花费的时间（或者所需步骤的数目）可以被求得：T(n) = 4n^2 - 2n + 2。
当 n 增大时，n^2; 项将开始占主导地位，而其他各项可以被忽略——举例说明：当 n = 500，4n^2; 项是 2n 项的1000倍大，因此在大多数场合下，省略后者对表达式的值的影响将是可以忽略不计的。

常数阶O(1)

常数又称定数，是指一个数值不变的常量，与之相反的是变量

为什么下面算法的时间复杂度不是O(3)，而是O(1)。

int sum = 0,n = 100; /*执行一次*/

sum = （1+n）*n/2; /*执行一次*/

printf（"%d", sum）; /*行次*/

这个算法的运行次数函数是f（n）=3。根据我们推导大O阶的方法，第一步就是把常数项3改为1。在保留最高阶项时发现，它根本没有最高阶项，所以这个算法的时间复杂度为O(1)。

另外，我们试想一下，如果这个算法当中的语句sum=（1+n）*n/2有10句，即：

int sum = 0, n = 100; /*执行1次*/

sum = （1+n）*n/2; /*执行第1次*/

sum = （1+n）*n/2; /*执行第2次*/

sum = （1+n）*n/2; /*执行第3次*/

sum = （1+n）*n/2; /*执行第4次*/

sum = （1+n）*n/2; /*执行第5次*/

sum = （1+n）*n/2; /*执行第6次*/

sum = （1+n）*n/2; /*执行第7次*/

sum = （1+n）*n/2; /*执行第8次*/

sum = （1+n）*n/2; /*执行第9次*/

sum = （1+n）*n/2; /*执行第10次*/

printf（"%d",sum）; /*执行1次*/

事实上无论n为多少，上面的两段代码就是3次和12次执行的差异。这种与问题的大小无关（n的多少），执行时间恒定的算法，我们称之为具有O(1)的时间复杂度，又叫常数阶。

注意：不管这个常数是多少，我们都记作O(1)，而不能是O(3)、O(12)等其他任何数字，这是初学者常常犯的错误。

O(n【时间规模，也可以理解为运行次数】)，当运算里没有最高阶项(也就是次方)时，时间规模就是1，所以为o(1),

如果运算里包含了最高阶项(也就是次方)时，且次方数不为1时，时间规模就是最高阶项(也就是次方数)，如o(3)，

推导大O阶方法

1.用常数1取代运行时间中的所有加法常数

2.在修改后的运行次数函数中，只保留最高阶项

3.如果最高阶项存在且不是1，则去除与这个项相乘的常数

对数阶O(log2n)　

对数

如果a的x次方等于N（a>0，且a不等于1），那么数x叫做以a为底N的对数（logarithm），记作x=logaN, 。其中，a叫做对数的底数，N叫做真数。
5^2 = 25 , 记作 2= log5 25
对数是一种运算，与指数是互逆的运算。例如

① 3^2=9 <==> 2=log<3>9；

② 4^(3/2)=8 <==> 3/2=log<4>8；

③ 10^n=35 <==> n=lg35。为了使用方便，人们逐渐把以10为底的常用对数记作lgN

对数阶

int count = 1;

while (count < n)

{

count = count * 2; /* 时间复杂度为O(1)的程序步骤序列 */

}

由于每次count乘以2之后，就距离n更近了一分。

也就是说，有多少个2相乘后大于n，则会退出循环。

由2^x=n得到x=log2n。所以这个循环的时间复杂度为O(logn)。

线性阶O(n)　　

执行时间随问题规模增长呈正比例增长

data = [ 8,3,67,77,78,22,6,3,88,21,2]

find_num = 22

for i in data:

if i == 22:

print("find",find_num,i )

线性对数阶O(nlog2n)

平方阶O(n^2)

for i in range(100):

for k in range(100):

print(i,k)

立方阶O(n^3)
k次方阶O(n^k),
指数阶O(2^n)。
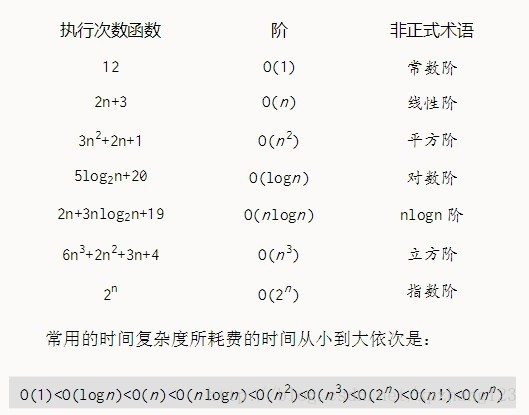
随着问题规模n的不断增大，上述时间复杂度不断增大，算法的执行效率越低。　　

一、计算方法

1.一个算法执行所耗费的时间，从理论上是不能算出来的，必须上机运行测试才能知道。但我们不可能也没有必要对每个算法都上机测试，只需知道哪个算法花费的时间多，哪个算法花费的时间少就可以了。并且一个算法花费的时间与算法中语句的执行次数成正比例，哪个算法中语句执行次数多，它花费时间就多。

一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)。

2.一般情况下，算法的基本操作重复执行的次数是模块n的某一个函数f（n），因此，算法的时间复杂度记做：T（n）=O（f（n））。随着模块n的增大，算法执行的时间的增长率和f（n）的增长率成正比，所以f（n）越小，算法的时间复杂度越低，算法的效率越高。

在计算时间复杂度的时候，先找出算法的基本操作，然后根据相应的各语句确定它的执行次数，再找出T（n）的同数量级（它的同数量级有以下：1，Log2n ，n ，nLog2n ，n的平方，n的三次方，2的n次方，n！），找出后，f（n）=该数量级，若T(n)/f(n)求极限可得到一常数c，则时间复杂度T（n）=O（f（n））。

3.常见的时间复杂度

按数量级递增排列，常见的时间复杂度有：

常数阶O(1),  对数阶O(log2n),  线性阶O(n),  线性对数阶O(nlog2n),  平方阶O(n^2)， 立方阶O(n^3),...， k次方阶O(n^k), 指数阶O(2^n) 。

其中，

1.O(n)，O(n^2)， 立方阶O(n^3),...， k次方阶O(n^k) 为多项式阶时间复杂度，分别称为一阶时间复杂度，二阶时间复杂度。。。。

2.O(2^n)，指数阶时间复杂度，该种不实用

3.对数阶O(log2n),   线性对数阶O(nlog2n)，除了常数阶以外，该种效率最高

例：算法：

  for（i=1;i<=n;++i）

  {

     for(j=1;j<=n;++j)

     {

         c[ i ][ j ]=0; //该步骤属于基本操作 执行次数：n^2

          for(k=1;k<=n;++k)

               c[ i ][ j ]+=a[ i ][ k ]*b[ k ][ j ]; //该步骤属于基本操作 执行次数：n^3

     }

  }

  则有 T（n）= n^2+n^3，根据上面括号里的同数量级，我们可以确定 n^3为T（n）的同数量级

  则有f（n）= n^3，然后根据T（n）/f（n）求极限可得到常数c

  则该算法的 时间复杂度：T（n）=O（n^3)

四、

定义：如果一个问题的规模是n，解这一问题的某一算法所需要的时间为T(n)，它是n的某一函数 T(n)称为这一算法的“时间复杂性”。

当输入量n逐渐加大时，时间复杂性的极限情形称为算法的“渐近时间复杂性”。

我们常用大O表示法表示时间复杂性，注意它是某一个算法的时间复杂性。大O表示只是说有上界，由定义如果f(n)=O(n)，那显然成立f(n)=O(n^2)，它给你一个上界，但并不是上确界，但人们在表示的时候一般都习惯表示前者。

此外，一个问题本身也有它的复杂性，如果某个算法的复杂性到达了这个问题复杂性的下界，那就称这样的算法是最佳算法。

“大O记法”：在这种描述中使用的基本参数是 n，即问题实例的规模，把复杂性或运行时间表达为n的函数。这里的“O”表示量级 (order)，比如说“二分检索是 O(logn)的”,也就是说它需要“通过logn量级的步骤去检索一个规模为n的数组”记法 O ( f(n) )表示当 n增大时，运行时间至多将以正比于 f(n)的速度增长。

这种渐进估计对算法的理论分析和大致比较是非常有价值的，但在实践中细节也可能造成差异。例如，一个低附加代价的O(n2)算法在n较小的情况下可能比一个高附加代价的 O(nlogn)算法运行得更快。当然，随着n足够大以后，具有较慢上升函数的算法必然工作得更快。

O(1)

Temp=i;i=j;j=temp;

以上三条单个语句的频度均为1，该程序段的执行时间是一个与问题规模n无关的常数。算法的时间复杂度为常数阶，记作T(n)=O(1)。如果算法的执行时间不随着问题规模n的增加而增长，即使算法中有上千条语句，其执行时间也不过是一个较大的常数。此类算法的时间复杂度是O(1)。

O(n^2)

2.1. 交换i和j的内容
     sum=0；                 （一次）
     for(i=1;i<=n;i++)       （n次）
        for(j=1;j<=n;j++) （n^2次）
         sum++；       （n^2次）
解：T(n)=2n^2+n+1 =O(n^2)

2.2.
    for (i=1;i<n;i++)
    {
        y=y+1;         ①
        for (j=0;j<=(2*n);j++)
           x++;        ②
    }
解：语句1的频度是n-1
          语句2的频度是(n-1)*(2n+1)=2n^2-n-1
          f(n)=2n^2-n-1+(n-1)=2n^2-2
          该程序的时间复杂度T(n)=O(n^2).

O(n)

2.3.
    a=0;
    b=1;                      ①
    for (i=1;i<=n;i++) ②
    {
       s=a+b;　　　　③
       b=a;　　　　　④
       a=s;　　　　　⑤
    }
解：语句1的频度：2,
           语句2的频度： n,
          语句3的频度： n-1,
          语句4的频度：n-1,
          语句5的频度：n-1,
          T(n)=2+n+3(n-1)=4n-1=O(n).

O(log2n )

2.4.
     i=1;       ①
    while (i<=n)
       i=i*2; ②
解：语句1的频度是1,
          设语句2的频度是f(n),   则：2^f(n)<=n;f(n)<=log2n
          取最大值f(n)= log2n,
          T(n)=O(log2n )

O(n^3)

2.5.
    for(i=0;i<n;i++)
    {
       for(j=0;j<i;j++)
       {
          for(k=0;k<j;k++)
             x=x+2;
       }
    }
解：当i=m, j=k的时候,内层循环的次数为k当i=m时, j 可以取 0,1,...,m-1 , 所以这里最内循环共进行了0+1+...+m-1=(m-1)m/2次所以,i从0取到n, 则循环共进行了: 0+(1-1)*1/2+...+(n-1)n/2=n(n+1)(n-1)/6所以时间复杂度为O(n^3).

我们还应该区分算法的最坏情况的行为和期望行为。如快速排序的最坏情况运行时间是 O(n^2)，但期望时间是 O(nlogn)。通过每次都仔细地选择基准值，我们有可能把平方情况 (即O(n^2)情况)的概率减小到几乎等于 0。在实际中，精心实现的快速排序一般都能以 (O(nlogn)时间运行。
下面是一些常用的记法：

访问数组中的元素是常数时间操作，或说O(1)操作。一个算法如果能在每个步骤去掉一半数据元素，如二分检索，通常它就取 O(logn)时间。用strcmp比较两个具有n个字符的串需要O(n)时间。常规的矩阵乘算法是O(n^3)，因为算出每个元素都需要将n对元素相乘并加到一起，所有元素的个数是n^2。
指数时间算法通常来源于需要求出所有可能结果。例如，n个元素的集合共有2n个子集,所以要求出所有子集的算法将是O(2n)的。指数算法一般说来是太复杂了，除非n的值非常小，因为，在这个问题中增加一个元素就导致运行时间加倍。不幸的是，确实有许多问题 (如著名的“巡回售货员问题” )，到目前为止找到的算法都是指数的。如果我们真的遇到这种情况，通常应该用寻找近似最佳结果的算法替代之。