【loj3056】【hnoi2019】多边形

题目

描述

​ 给出一个 \(n\) 个点的多边形初始的三角剖分；

​ 一次合法的旋转定义为 \((a,b,c,d)\) ，满足 \(a<b<c<d\) ；

​ 并且存在边\((a,b)(b,c)(c,d)(d,a)(a,c)\) ，将 \((a,c) - > (b,d)\) ;

​ 简化后用\((a,c)\)描述一次旋转；

​ 给出 \(m\) 个旋转操作，表示每次从初始状态 \(S_0\) 旋转成 \(S_i\) ；

​ 询问对于 \(S_0 - S_m\) 到不能旋转的最少的步数以及方案数；

范围

​ $ 3 \le n \le 10^5 \ , \ 0 \le m \le 10^5 $ ;

题解

• 无法再旋转的情况为所有点的某一个端点都是 \(n\) , 否则所有连向 \(n\) 的边会将所有的多边形划分成很多部分，每个部分相互独立，并且每个部分里面一定可以再次移动。我们知道答案的一个下界是两个端点都不为 \(n\) 的线段条数，这个下界是可以达到的：可以发现每部分里面所有的区间形成了一个二叉树的结构，每次从根节点开始操作旋转，可以直接让根的某个端点到 \(n\)，此时左右次数变成了新的两个独立的部分，再继续操作其左右子树。

• 接下来将每条连线 \((a,b)\) 看成线段，单调栈求出这个二叉树森林，显然最小步数==节点数 。 考虑方案，对于每一个二叉树，先转子树是无效的。所以合法的方案=> <优先选根，再选左右子树> 方案数是 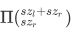。将二叉森林组合起来类似地乘以一个组合数即可；

• 加入修改，对于一次从 \(S_0\) 的改变，对旋转线段对应的点 \(u\) ，分两种情况讨论：

  • \(u\) 为某个二叉树的根，最小次数--，删去根，左右儿子被分裂成了两个新的子树统计方案；
  • 否则由于要合法一定是父亲的左儿子，最小次数不变，left-rotate(u) 之后统计方案(可以自己画图。。)；

• 均可以只考虑变化量 \(O(1)\) 做到，考虑到要lower_bound旋转线段的标号：\(O(n \log n)\) ;

• 最近状态好迷啊，交了一发$WA $ 了，改了半天发现没取模TAT，点开博客看看其他人的做法发现yyb神仙也没有取模OVO ；

  #include<bits/stdc++.h>
  #define ll long long
  using namespace std;
  const int N=200010,mod=1e9+7;
  int Case,n,m,cnt,st[N],top,ls[N],rs[N],fa[N],sz[N],id[N],pre=1,fac[N],inv[N],iv[N];
  struct data{
  	int l,r;
  	data(int _l=0,int _r=0):l(_l),r(_r){};
  	bool operator <(const data&A)const{return r==A.r?l>A.l:r<A.r;}
  }A[N];
  char gc(){
  	static char*p1,*p2,s[1000000];
  	if(p1==p2)p2=(p1=s)+fread(s,1,1000000,stdin);
  	return(p1==p2)?EOF:*p1++;
  }
  int rd(){
  	int x=0;char c=gc();
  	while(c<'0'||c>'9')c=gc();
  	while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+c-'0',c=gc();
  	return x;
  }
  char ps[1000000],*pp=ps;
  void push(char x){
  	if(pp==ps+1000000)fwrite(ps,1,1000000,stdout),pp=ps;
  	*pp++=x;
  }
  void flush(){fwrite(ps,1,pp-ps,stdout);pp=ps;}
  void write(int x){
  	static int sta[20],top;
  	if(!x){push('0');return;}
  	while(x)sta[++top]=x%10,x/=10;
  	while(top)push(sta[top--]^'0');
  }
  int cal(int x,int y){return 1ll*fac[x+y]*inv[x]%mod*inv[y]%mod;}
  int ical(int x,int y){return 1ll*inv[x+y]*fac[x]%mod*fac[y]%mod;}
  void pushup(int x){
  	int l=ls[x],r=rs[x];
  	sz[x]=sz[l]+sz[r]+1;
  	pre=1ll*pre*cal(sz[l],sz[r])%mod;
  }
  int mfy1(int x){
  	int re=pre,l=ls[x],r=rs[x];
  	re=1ll*re*ical(cnt-sz[x],sz[x])%mod*ical(sz[l],sz[r])%mod;
  	re=1ll*re*cal(cnt-sz[x],sz[l])%mod*cal(cnt-1-sz[r],sz[r])%mod;
  	return re;
  }
  int mfy2(int x){
  	int re=pre,y=fa[x];
  	re=1ll*re*ical(sz[ls[y]],sz[rs[y]])%mod*ical(sz[ls[x]],sz[rs[x]])%mod;
  	re=1ll*re*cal(sz[y]-1-sz[ls[x]],sz[ls[x]])%mod*cal(sz[rs[x]],sz[rs[y]])%mod;
  	return re;
  }
  int main(){
  //	freopen("polygon.in","r",stdin);
  //	freopen("polygon.out","w",stdout);
  	Case=rd();n=rd();
  	iv[1]=1;for(int i=2;i<=n;++i)iv[i]=(ll)(mod-mod/i)*iv[mod%i]%mod;
  	for(int i=fac[0]=inv[0]=1;i<=n;++i){
  		fac[i]=(ll)fac[i-1]*i%mod;
  		inv[i]=(ll)inv[i-1]*iv[i]%mod;
  	}
  	for(int i=1;i<=n-3;++i){
  		A[i].l=rd(),A[i].r=rd();
  		if(A[i].l>A[i].r)swap(A[i].l,A[i].r);
  	}
  	sort(A+1,A+n-2);
  	for(int i=1;i<=n-3;++i){
  		if(A[i].r==n)break;
  		id[i]=++cnt;
  		while(top&&A[st[top]].l>=A[i].l){
  			if(A[st[top]].l==A[i].l)ls[cnt]=id[st[top--]],fa[ls[cnt]]=cnt;
  			else rs[cnt]=id[st[top--]],fa[rs[cnt]]=cnt;
  		}
  		pushup(cnt);st[++top]=i;
  	}
  	for(int i=1,tmp=0;i<=top;++i){
  		int t=sz[id[st[i]]];
  		pre=1ll*pre*cal(tmp,t)%mod;
  		tmp+=t;
  	}
  	m=rd();
  	write(cnt);if(Case){push(' ');write(pre);}push('\n');
  	for(int i=1,x,y,p,ans1,ans2;i<=m;++i){
  		x=rd(),y=rd();if(x>y)swap(x,y);
  		p = id[ lower_bound(A+1,A+n-2,data(x,y)) - A ];
  		if(!fa[p]){ans1=cnt-1;ans2=mfy1(p);}
  		else {ans1=cnt;ans2=mfy2(p);}
  		write(ans1);if(Case){push(' ');write(ans2);}push('\n');
  	}
  	flush();
  	return 0;
  }