利用Tarjan算法解决（LCA）二叉搜索树的最近公共祖先问题——数据结构

相关知识：（来自百度百科）

 LCA（Least Common Ancestors）

即最近公共祖先，是指在有根树中，找出某两个结点u和v最近的公共祖先。

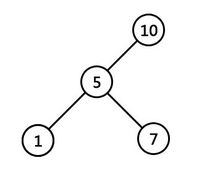
例如：

1和7的最近公共祖先为5；

1和5的最近公共祖先为5；

7和5的最近公共祖先为7；

---

题目：

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。

例如，给定如下二叉搜索树:  root = [6,2,8,0,4,7,9,null,null,3,5]

示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。

示例 2:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

说明:

• 所有节点的值都是唯一的。
• p、q 为不同节点且均存在于给定的二叉搜索树中。

---

常见解法：

1.暴力枚举（朴素算法）

遍历树，找到两个节点（A、B）的位置。

将深度较深的节点（A）向树的根部移动到和深度较浅的节点（B）同一深度。

然后两个点一起向上移动，直到重叠。

2.运用DFS序

3.倍增寻找（ST算法）

4.Tarjan算法（离线算法）

5.树链剖分

---

分析：

这里讨论一下Tarjan算法（因为只看懂了这个）

Tarjan算法其实是一种由Robert Tarjan提出的求解有向图强连通分量的线性时间的算法。

如果把LCA看作一个图的话，就是求连接图中两个元素的最短路径。

而这个算法是基于并查集（两个元素是否同一上级）和DFS（深度优先搜索）

DFS的作用是深度遍历整个树，并查集的作用是将该点和其子节点连接成一个集合：如下图每种颜色代表一个集合

个人的理解：

① 如果在上图中找2和8的最近公共祖先，从根节点1开始深度遍历，会首先得到蓝色这个集合（2在集合中）。

② 但在遍历的过程中发现蓝色集合里面没有8，那么就说明8在其他颜色的集合里面。

③ 而蓝色集合与其他颜色集合连接点为1，不用考虑8在哪个集合中，就能够断定2和8的最近公共祖先是1。

---

Tarjan代码实现：

/**
 * 对二叉树节点的定义
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
 
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
 
        if(root == NULL)//若根节点为空，返回NULL
            return NULL;
        if(root == p || root == q)//当q为p的父节点或p为q的父节点
            return root;
 
        //这里通过递归实现LCA
        TreeNode* left = lowestCommonAncestor(root->left, p, q);
        TreeNode* right = lowestCommonAncestor(root->right, p, q);
 
        if(left != NULL && right != NULL)
            return root;
        else if(left != NULL)
            return left;//移到节点的左孩子
        else if(right != NULL)
            return right;//移到节点的右孩子
        else
            return NULL;
 
    }
};