图->最短路径->单源最短路径(迪杰斯特拉算法Dijkstra)

文字描述

　　引言：如下图一个交通系统，从A城到B城，有些旅客可能关心途中中转次数最少的路线，有些旅客更关心的是节省交通费用，而对于司机，里程和速度则是更感兴趣的信息。上面这些问题，都可以转化为求图中，两顶点最短带权路径的问题。

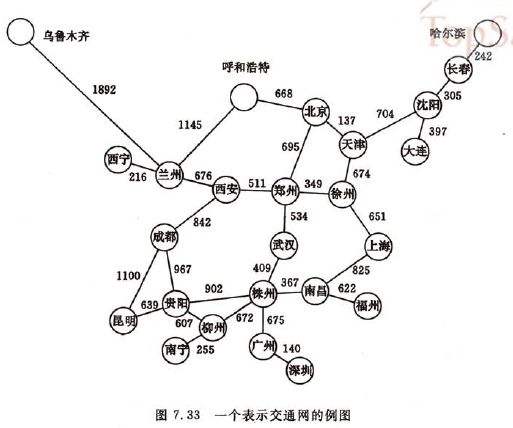
　　单源点的最短路径问题: 给定带权有向图G和源点v，求从v到G中其余各顶点的最短路径。迪杰斯特拉(Dijkstra)提出了一个按路径长度递增的次序产生最短路径的算法。迪杰斯特拉(Dijkstra)算法描述如下：

　　

示意图

　　

　　

　　

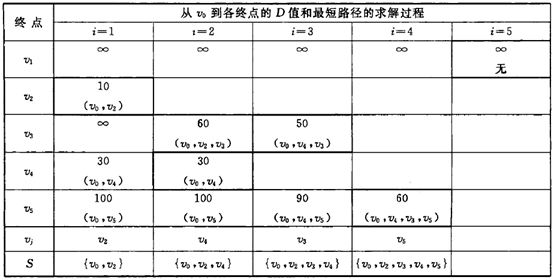
算法分析

　　结合代码实现部分分析这个算法的运行时间。本博客写的代码,其时间复杂度为n^3, 但是理论上应该只为n^2

代码实现

 //
 // Created by lady on 19-1-3.
 //
 #include <stdio.h>
 #include <stdlib.h>

 #define INFINITY        100000    //最大值
 #define MAX_VERTEX_NUM    20        //最大顶点数
 typedef enum {DG, DN, UDG, UDN} GraphKind; //{有向图，有向网，无向图，无向网}
 typedef struct ArcCell{
     int weight;    //该弧相关信息的指针
 }ArcCell, AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM], PathMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM], ShortPathTable[MAX_VERTEX_NUM];
 typedef struct VertexType{
     char data[];
 }VertexType;
 typedef struct{
     VertexType vexs[MAX_VERTEX_NUM];    //顶点向量
     AdjMatrix arcs;        //邻接矩阵
     int vexnum, arcnum;    //图的当前顶点数和弧数
     GraphKind kind;        //图的种类标志
 }MGraph;

 /*
  * 根据顶点信息， 返回该顶点在图中的位置， 如果返回-1表示顶点不存在
  */
 static int LocateVex(MGraph *G, char data[])
 {
     int i = ;
     for(i=; i<G->vexnum; i++){
         if(!strncmp(G->vexs[i].data, data, strlen(G->vexs[i].data))){
             return i;
         }
     }
     return -;
 }

 /*
  * 用邻接矩阵作为存储结构，创建有向网
  */
 static int CreateGraphDN(MGraph *G)
 {
     printf("用邻接矩阵创建有向网,输入顶点数，弧数：");
     G->kind = DN;
     scanf("%d,%d", &G->vexnum, &G->arcnum);
     if(G->vexnum > MAX_VERTEX_NUM){
         printf("错误:顶点数不能超过%d!!\n", MAX_VERTEX_NUM);
         return -;
     }
     int i = , j = , k = ;
     char v1[] = {}, v2[]={}, info[] = {};
     char tmp[] = {};
     for(i=; i<G->vexnum; i++){
         printf("输入第%d个顶点: ", i);
         memset(G->vexs[i].data, , sizeof(G->vexs[].data));
         scanf("%s", G->vexs[i].data);
         for(j=; j<G->vexnum; j++){
             G->arcs[i][j].weight = INFINITY;
         }
         G->arcs[i][i].weight = ;
     }
     for(k=; k<G->arcnum; k++){
         printf("输入第%d条弧(顶点1, 顶点2): ", k);
         memset(tmp, , sizeof(tmp));
         scanf("%s", tmp);
         sscanf(tmp, "%[^','],%[^','],%s[^\\n]", v1, v2, info);
         i = LocateVex(G, v1);
         j = LocateVex(G, v2);
         if(i< || j< || (!atoi(info))){
             printf("错误:顶点%s或者%s不存在, 或者权值信息%s不对!\n", v1, v2, info);
             return -;
         }
         G->arcs[i][j].weight = atoi(info);
     }
     return ;
 }
 static void printMatrix(int vexnum, VertexType vexs[], int (*arcs)[MAX_VERTEX_NUM])
 {
     int i = , j = ;
     printf("\t");
     for(i=; i<vexnum; i++){
         printf("%s\t", vexs[i].data);
     }
     printf("\n");
     for(i=; i<vexnum; i++){
         printf("%s\t", vexs[i].data);
         for(j=; j<vexnum; j++){
             if(arcs[i][j] == INFINITY){
                 printf("INF\t");
             }else{
                 printf("%d\t", arcs[i][j]);
             }
         }
         printf("\n");
     }
     return ;
 }

 static void printArchs(int vexnum, VertexType vexs[], AdjMatrix arcs)
 {
     int i = , j = ;
     printf("\t");
     for(i=; i<vexnum; i++){
         printf("%s\t", vexs[i].data);
     }
     printf("\n");
     for(i=; i<vexnum; i++){
         printf("%s\t", vexs[i].data);
         for(j=; j<vexnum; j++){
             if(arcs[i][j].weight == INFINITY){
                 printf("INF\t");
             }else{
                 printf("%d\t", arcs[i][j].weight);
             }
         }
         printf("\n");
     }
     return ;
 }

 #include <string.h>
 /*
  * Dijkstra迪杰斯特拉算法
  * 从有向网G的顶点v0出发，求v0到其余顶点v的最短路径P[v]及其带权长度D[v].weight
  * 若P[v][w].weight为TRUE(1)，则w是从v0到v当前求得最短路径上的顶点。
  * final[v]为TRUE(1)，当且仅当v属于S，即已经求得从v0到v的最短路径
  */
 void ShortestPath_DIJ(MGraph *G, int v0)
 {
     int v = ;
     int w = ;
     int i = ;
     int j = ;
     int final[MAX_VERTEX_NUM] = {};
     int min = ;
     int P[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
     ShortPathTable D;

     for(v=; v<G->vexnum; ++v){
         D[v].weight = G->arcs[v0][v].weight;
         //设为空路径
         for(w=; w<G->vexnum; ++w){
             P[v][w] = ;
         }
         if(D[v].weight < INFINITY){
             P[v][v0] = ;
             P[v][v] = ;
         }
     }
     //初始化，v0顶点属于S集
     D[v0].weight = ;
     final[v0] = ;
     //开始主循环，每次求得v0到某个v顶点的最短路径，并加v到s集
     //其余G->vexnum-1个顶点
     for(i=; i<G->vexnum; ++i){
         //min存放当前离v0顶点最短的距离
         min = INFINITY;
         for(w=; w<G->vexnum; w++){
             if(!final[w]){
                 //顶点w在V-S中
                 if(D[w].weight < min){
                     //顶点v0更近
                     min = D[w].weight;
                     v = w;
                 }
             }
         }
         if(min == INFINITY)
             break;
         //离v0最短的顶点v加入S集合
         final[v] = ;
         //更新当前最短路径和距离
         for (w = ; w < G->vexnum; w++) {
             if (!final[w] && (min + G->arcs[v][w].weight < D[w].weight)) {
                 //修改D[w]和P[w]，w属于V-S
                 D[w].weight = min + G->arcs[v][w].weight;
                 for(j=; j<G->vexnum; j++){
                     P[w][j] = P[v][j];
                 }
                 P[w][w] = ;
             }
         }
     }

     printf("\n打印最短路径:\n");
     printMatrix(G->vexnum, G->vexs, P);

     printf("\n打印%s到其余顶点的带权长度:\n", G->vexs[v0].data);
     for(i=; i<G->vexnum; i++){
         if(D[i].weight == INFINITY){
             printf("%s,INF\t", G->vexs[i].data);
         }else {
             printf("%s,%d\t", G->vexs[i].data, D[i].weight);
         }
     }
     printf("\n");
     return ;
 }

 int main(int argc, char *argv[])
 {
     //以邻接矩阵为存储结构创建有向网
     MGraph G;
     if(CreateGraphDN(&G) < ){
         return -;
     }
     printf("\n打印该图中的信息:\n");
     printArchs(G.vexnum, G.vexs, G.arcs);
     //Dijkstra迪杰斯特拉算法求单源最短路径
     ShortestPath_DIJ(&G, );
     return ;
 }

单源最短路径(Dijkstra)

代码运行

/home/lady/CLionProjects/untitled/cmake-build-debug/untitled
用邻接矩阵创建有向网,输入顶点数，弧数：6,8
输入第0个顶点: v0
输入第1个顶点: v1
输入第2个顶点: v2
输入第3个顶点: v3
输入第4个顶点: v4
输入第5个顶点: v5
输入第0条弧(顶点1, 顶点2): v0,v5,100
输入第1条弧(顶点1, 顶点2): v0,v4,30
输入第2条弧(顶点1, 顶点2): v0,v2,10
输入第3条弧(顶点1, 顶点2): v1,v2,5
输入第4条弧(顶点1, 顶点2): v2,v3,50
输入第5条弧(顶点1, 顶点2): v4,v5,60
输入第6条弧(顶点1, 顶点2): v4,v3,20
输入第7条弧(顶点1, 顶点2): v3,v5,10

打印该图中的信息:
    v0    v1    v2    v3    v4    v5
v0    0    INF    10    INF    30    100
v1    INF    0    5    INF    INF    INF
v2    INF    INF    0    50    INF    INF
v3    INF    INF    INF    0    INF    10
v4    INF    INF    INF    20    0    60
v5    INF    INF    INF    INF    INF    0    

打印最短路径:
    v0    v1    v2    v3    v4    v5
v0    1    0    0    0    0    0
v1    0    0    0    0    0    0
v2    1    0    1    0    0    0
v3    1    0    0    1    1    0
v4    1    0    0    0    1    0
v5    1    0    0    1    1    1    

打印v0到其余顶点的带权长度:
v0,0    v1,INF    v2,10    v3,50    v4,30    v5,60    

Process finished with exit code 0