java使用递归及迭代方式实现前序遍历 中序遍历 后序遍历 以及实现层序遍历

本文为博主原创，转载请注明出处：

　　目录：

　　　　一。快速理解前序，中序，后序遍历的区别

　　　　二。使用递归的方式实现前序，中序，后序遍历

　　　　三。 使用迭代的方式实现前序 中序 后序遍历

　　　　四。层序遍历

一。快速理解前序，中序，后序遍历的区别

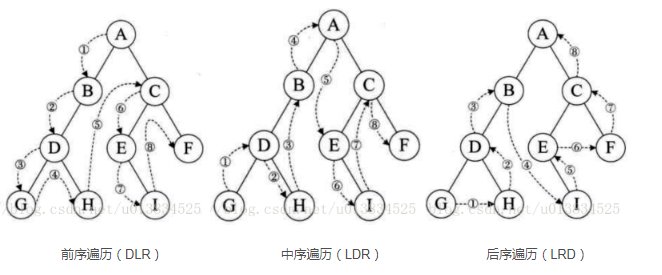
前序遍历：根左右（根在前，从左往右，一棵树的根永远在左子树前面，左子树又永远在右子树前面 ）

中序遍历：左根右（根在中，从左往右，一棵树的左子树永远在根前面，根永远在右子树前面）

后序遍历：左右根（根在后，从左往右，一棵树的左子树永远在右子树前面，右子树永远在根前面）

参考一张图可以快速理解三种遍历的顺序

二。使用递归的方式实现前序，中序，后序遍历

package com.example.test.tree;

public class TreeNode {
    // 树的根结点值
    int val;
    // 根节点对应的左节点
    TreeNode left = null;
    // 根节点对应的右节点
    TreeNode right = null;
    public TreeNode(int val){
        this.val = val;
    }

    /**
     * 树的前序便利：根节点--〉左节点---〉右节点
     * @param root
     */
    public static void preOrder(TreeNode root) {
        if (root == null) {
            return;
        }
        System.out.print(root.val + "   ");
        preOrder(root.left);
        preOrder(root.right);
    }

    /**
     * 树的中序遍历 ： 左节点--〉中节点 --〉 右节点
     * @param root
     */
    public static void middleOrder(TreeNode root){
        if (root ==null){return;}
        middleOrder(root.left);
        System.out.print(root.val+ "   ");
        middleOrder(root.right);
    }

    /**
     * 树的后序遍历： 左节点--〉右节点 --> 根节点
     * @param root
     */
    public static void afterOrder(TreeNode root){
        if (root == null){return;}
        afterOrder(root.left);
        afterOrder(root.right);
        System.out.print(root.val+ "   ");
    }

    public static void main(String[] args) {
        TreeNode root = new TreeNode(20);
        TreeNode node1 = new TreeNode(4);
        TreeNode node2 = new TreeNode(5);
        TreeNode node3 = new TreeNode(8);
        TreeNode node4 = new TreeNode(2);
        TreeNode node5 = new TreeNode(7);
        TreeNode node6 = new TreeNode(12);
        TreeNode node7 = new TreeNode(3);
        TreeNode node8 = new TreeNode(9);
        root.left = node1;
        root.right = node2;
        node1.left = node3;
        node1.right = node4;
        node2.left = node5;
        node2.right = node6;
        node3.left = node7;
        node4.right = node8;
        preOrder(root);
        System.out.println();
        middleOrder(root);
        System.out.println();
        afterOrder(root);
    }

}

三。 使用迭代的方式实现前序 中序 后序遍历

package com.example.test.tree;

import java.util.Stack;

public class TreeNode {
    // 树的根结点值
    int val;
    // 根节点对应的左节点
    TreeNode left = null;
    // 根节点对应的右节点
    TreeNode right = null;

    public TreeNode(int val) {
        this.val = val;
    }

    /**
     * 前序遍历：使用stack 记录递归路径，须保证左子节点先出栈
     *
     * @param root
     */
    public static void preOrder2(TreeNode root) {
        if (root != null) {
            Stack<TreeNode> stack = new Stack<>();
            stack.add(root);
            while (!stack.isEmpty()) {
                root = stack.pop();
                if (root != null) {
                    System.out.print(root.val + "   ");
                    stack.push(root.right);
                    stack.push(root.left);
                }
            }
        }
    }

    /**
     * 中序遍历：将左子节点入栈，出栈打印值，然后添加右子节点
     *
     * @param root
     */
    public static void middleOrder2(TreeNode root) {
        if (root != null) {
            Stack<TreeNode> stack = new Stack<>();
            while (!stack.isEmpty() || root != null)
                if (root != null) {
                    stack.push(root);
                    root = root.left;
                } else {
                    root = stack.pop();
                    System.out.print(root.val + "   ");
                    root = root.right;
                }
        }
    }

    /**
     * 后序遍历
     * @param root
     */
    public void afterOrder2(TreeNode root) {
        TreeNode cur, pre = null;

        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);

        while (!stack.empty()) {
            cur = stack.peek();
            if ((cur.left == null && cur.right == null) || (pre != null && (pre == cur.left || pre == cur.right))) {
                System.out.print(cur.val + "->");
                stack.pop();
                pre = cur;
            } else {
                if (cur.right != null)
                    stack.push(cur.right);
                if (cur.left != null)
                    stack.push(cur.left);
            }
        }
    }

    public static void main(String[] args) {
        TreeNode root = new TreeNode(20);
        TreeNode node1 = new TreeNode(4);
        TreeNode node2 = new TreeNode(5);
        TreeNode node3 = new TreeNode(8);
        TreeNode node4 = new TreeNode(2);
        TreeNode node5 = new TreeNode(7);
        TreeNode node6 = new TreeNode(12);
        TreeNode node7 = new TreeNode(3);
        TreeNode node8 = new TreeNode(9);
        root.left = node1;
        root.right = node2;
        node1.left = node3;
        node1.right = node4;
        node2.left = node5;
        node2.right = node6;
        node3.left = node7;
        node4.right = node8;
        preOrder2(root);
        System.out.println();
        middleOrder2(root);
        System.out.println();
        afterOrder2(root);
    }

}

四。层序遍历

 /**
     * 层序遍历
     * @param root
     */
    public static void levelOrder(TreeNode root) {
        if (root == null) {
            return;
        }
        Queue<TreeNode> queue = new LinkedList<TreeNode>();
        queue.add(root);
        while (!queue.isEmpty()) {
            TreeNode node = queue.poll();
            System.out.print(node.val + "->");

            if (node.left != null) {
                queue.add(node.left);
            }
            if (node.right != null) {
                queue.add(node.right);
            }
        }

    }