Lucas定理 、斯特灵公式

斯特灵公式是一条用来取n阶乘的近似值的数学公式。

公式为：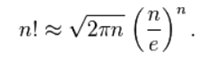

用该公式我们可以用来估算n阶乘的值；估算n阶乘的在任意进制下的位数。

如何计算在R进制下的位数：我们可以结合对数来计算，比如十进制就是lg（n！）+1，二进制则是log2（n！）+1。

Lucas（卢卡斯）定理

公式为：

当然，当n较小时，我们可以用组合数里面的定理来递推求解。

然而当n较大时，显然时间花费很大。而Lucas定理恰好是解决大组合数取模的优解。

在这里由于知识有限，不能完全看懂Lucas定理证明的全部过程。所以就不写了。

而代码实现Lucas定理也很简洁。只需要递归就行。

使用Lucas定理的时候需要注意：p不能太大于10^5。

Cnm=Cn/pm/p×Cnmodpmmodp(modp)。

Cnm=Cn/pm/p×Cnmodpmmodp(modp)。

Cnm=Cn/pm/p×Cnmodpmmodp(modp)。