洛谷——P1038 神经网络

P1038 神经网络

题目背景

人工神经网络（Artificial Neural Network）是一种新兴的具有自我学习能力的计算系统，在模式识别、函数逼近及贷款风险评估等诸多领域有广泛的应用。对神经网络的研究一直是当今的热门方向，兰兰同学在自学了一本神经网络的入门书籍后，提出了一个简化模型，他希望你能帮助他用程序检验这个神经网络模型的实用性。

题目描述

在兰兰的模型中，神经网络就是一张有向图，图中的节点称为神经元，而且两个神经元之间至多有一条边相连，下图是一个神经元的例子：

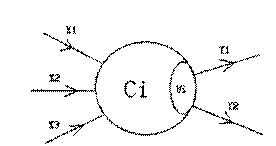
神经元〔编号为1）

图中，X1―X3是信息输入渠道，Y1－Y2是信息输出渠道，C1表示神经元目前的状态，Ui是阈值，可视为神经元的一个内在参数。

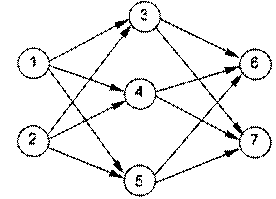
神经元按一定的顺序排列，构成整个神经网络。在兰兰的模型之中，神经网络中的神经无分为几层；称为输入层、输出层，和若干个中间层。每层神经元只向下一层的神经元输出信息，只从上一层神经元接受信息。下图是一个简单的三层神经网络的例子。

兰兰规定，Ci服从公式：（其中n是网络中所有神经元的数目）

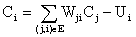
公式中的Wji（可能为负值）表示连接j号神经元和 i号神经元的边的权值。当 Ci大于0时，该神经元处于兴奋状态，否则就处于平静状态。当神经元处于兴奋状态时，下一秒它会向其他神经元传送信号，信号的强度为Ci。

如此．在输入层神经元被激发之后，整个网络系统就在信息传输的推动下进行运作。现在，给定一个神经网络，及当前输入层神经元的状态（Ci），要求你的程序运算出最后网络输出层的状态。

输入输出格式

输入格式：

输入文件第一行是两个整数n（1≤n≤100）和p。接下来n行，每行两个整数，第i＋1行是神经元i最初状态和其阈值（Ui），非输入层的神经元开始时状态必然为0。再下面P行，每行由两个整数i，j及一个整数Wij，表示连接神经元i、j的边权值为Wij。

输出格式：

输出文件包含若干行，每行有两个整数，分别对应一个神经元的编号，及其最后的状态，两个整数间以空格分隔。仅输出最后状态大于零的输出层神经元状态，并且按照编号由小到大顺序输出！

若输出层的神经元最后状态均为 0，则输出 NULL。

输入输出样例

输入样例#1：

5 6
1 0
1 0
0 1
0 1
0 1
1 3 1
1 4 1
1 5 1
2 3 1
2 4 1
2 5 1

输出样例#1：

3 1
4 1
5 1

拓扑排序我们需要弄明白这样一点：输入层是指入度为零的点，输出层是指出度为零的点。所以我们需要处理入度为零的点和出度为零的点。然后在进行拓扑排序，在拓扑排序里面的时候我们要注意题目中有个要求：当 Ci大于0时，该神经元处于兴奋状态，否则就处于平静状态。当神经元处于兴奋状态时，下一秒它会向其他神经元传送信号，信号的强度为Ci。也就是说当c[i]<0的时候我们就不在进行信息传递，直接break。天呐，蒟蒻竟然弄了半天也没弄懂那个公式是什么意思、、、、一直认为是讲他们乘起来然后减u[i]然后在累加、、、结果他没有括号、、、（也就是说他不是每次都减、、、）只减一次，我们如果在拓扑排序里面减的话就把入度为零的也减去了。那就在外面减吧、、、某大佬原话：有阈值的神经元一定有入读，一定是从一个入度为零的神经元得到的，continue得时候，不会把你刚开始减过阈值的神经元过滤，因为那时候她还有入读你可以最开始把有入读的点的阈值减去。然后在更新得时候就不用管阈值了

#include<queue>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 1100
using namespace std;
bool flag;
int n,m,x,y,z,tot,c[N],u[N],in[N],out[N],head[N];
queue<int>q;
int read()
{
    ,f=; char ch=getchar();
    ; ch=getchar();}
    +ch-'; ch=getchar();}
    return x*f;
}
struct Edge
{
    int to,dis,next;
}edge[N];
int add(int x,int y,int z)
{
    tot++;
    edge[tot].to=y;
    edge[tot].dis=z;
    edge[tot].next=head[x];
    head[x]=tot;
}
int main()
{
    n=read(),m=read();
    ;i<=n;i++)
     c[i]=read(),u[i]=read();
    ;i<=m;i++)
    {
        x=read(),y=read(),z=read();
        add(x,y,z),in[y]++,out[x]++;
    }
    ;i<=n;i++)
      if(in[i]) c[i]-=u[i];
    ;i<=n;i++)
     if(!in[i]) q.push(i);
    while(!q.empty())
    {
        int x=q.front();q.pop();
        ) continue;
        for(int i=head[x];i;i=edge[i].next)
        {
            int t=edge[i].to;
            in[t]--;
            c[t]+=c[x]*edge[i].dis;
            ) q.push(t);
        }
     }
     ;i<=n;i++)
      ) flag=,printf("%d %d\n",i,c[i]);
     if(!flag) printf("NULL\n");
     ;
}