appium学习【五】【转】appium实现屏幕向左滑动

转自http://www.cnblogs.com/testhub/p/5949668.html

前些日子写一个滑动手机页面的小脚本，看到大家给的内容都是swipe方法，这里对swipe方法做一个小介绍：

Swipe（int start x,int start y,int end x,int y,duration)

解释：int start x－开始滑动的x坐标，

int start y －开始滑动的y坐标。

int end x －结束点x坐标，

int end y －结束点y坐标。

duration 滑动时间（默认5毫秒）；

由于swipe方法需要制定的是坐标，但是由于每个手机的分辨率不同，如果我们指定了一个固定的坐标，在其他手机上也不一定能适用，所以最好的办法就是通过获取手机屏幕的坐标来滑动，

这样可以增加代码的复用性。

以下是我的python代码：

dr=webdriver.Remote("http://localhost:4725/wd/hub",desired_cups)

#获得机器屏幕大小x,y
def getSize():
    x = dr.get_window_size()['width']
    y = dr.get_window_size()['height']
    return (x, y)

#屏幕向上滑动
def swipeUp(t):
    l = getSize()
    x1 = int(l[0] * 0.5)    #x坐标
    y1 = int(l[1] * 0.75)   #起始y坐标
    y2 = int(l[1] * 0.25)   #终点y坐标
    dr.swipe(x1, y1, x1, y2,t)

简单解释一下：

下图是屏幕的坐标图，向上滑动屏幕就是x轴不变，y轴由大到小的变化过程

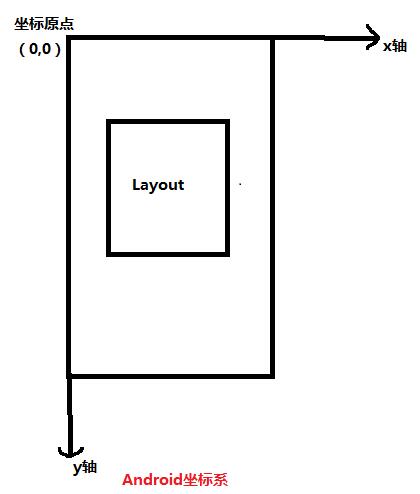
以下我将向上滑动、向下滑动、向左滑动和向右滑动整理了一下，并且实现他们的调用：

#获得机器屏幕大小x,y
def getSize():
    x = dr.get_window_size()['width']
    y = dr.get_window_size()['height']
    return (x, y)

#屏幕向上滑动
def swipeUp(t):
    l = getSize()
    x1 = int(l[0] * 0.5)  #x坐标
    y1 = int(l[1] * 0.75)   #起始y坐标
    y2 = int(l[1] * 0.25)   #终点y坐标
    dr.swipe(x1, y1, x1, y2,t)
#屏幕向下滑动
def swipeDown(t):
    l = getSize()
    x1 = int(l[0] * 0.5)  #x坐标
    y1 = int(l[1] * 0.25)   #起始y坐标
    y2 = int(l[1] * 0.75)   #终点y坐标
    dr.swipe(x1, y1, x1, y2,t)
#屏幕向左滑动
def swipLeft(t):
    l=getSize()
    x1=int(l[0]*0.75)
    y1=int(l[1]*0.5)
    x2=int(l[0]*0.05)
    dr.swipe(x1,y1,x2,y1,t)
#屏幕向右滑动
def swipRight(t):
    l=getSize()
    x1=int(l[0]*0.05)
    y1=int(l[1]*0.5)
    x2=int(l[0]*0.75)
    dr.swipe(x1,y1,x2,y1,t)
#调用向左滑动
swipLeft(1000)
sleep(3)
#调用向右滑动
swipRight(1000)
调用向上滑动
swipeUp(1000)
调用向下滑动
swipeDown(1000)