hihocoder 1584 Bounce (数学 && 规律) ACM-ICPC北京赛区2017网络赛

题意：

给定一副n*m的格子图， 问从左上角的点开始往右下角滑，碰到墙壁就反弹， 碰到角落就停止， 问恰好经过一次的格子有多少个。

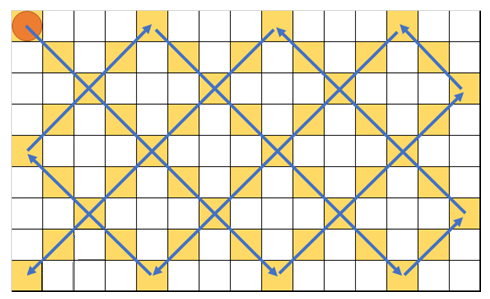
如图，恰好经过一次的格子有39个。

分析：

首先要引入两个概念， “路径长”，“格子数”。

路径长指的是整段路程的长度，如果走过同一个格子两次那么就算是2步。

格子数指的是整段路程经过的格子。

如果一个图是9*9（形如n*n）的， 那么就是从左上角一直到右下角， 走过的“路径长”恰好等于“格子数”，没有任何的格子被走过两次。

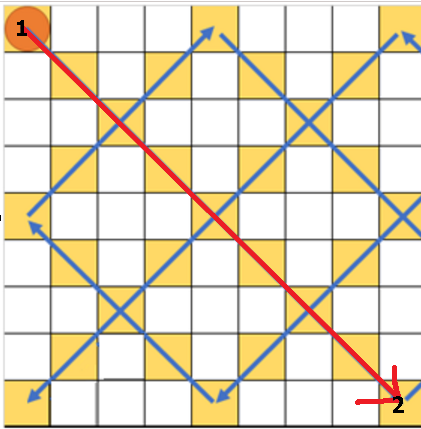
但对于一幅9 * 15这样不规则的图，“格子数”为“48”，“路径长”为57。

如果把格子都平移成一条直线的话， 那么有一些格子就会存在“共用”。上图中1~9号都成为“共用点”，其中“3、6、9”为行共用，“2、4、5、7、8、10”为列共用点，1和11分别给起点和终点。

只考虑1 - 2 - 3 - 4 - 5 - 6 这条连线， 如果把他们平移成行的话， 那么只有15 + 14的“路径长” ， 并非两行15*2 =30 “路径长”。 因为3号顶点是这两行共用的， 不能单独算。整幅图而言，因为行共用点有3个， 所以最后如果都算行平移的话会有15 + （15-1）*3 = 57“路径长”， 如果都算列平移同样会有9 + （9-1）*6 = 57“路径长”。

那么我们考虑将一个n*m的“路径长”，放大成最小倍数使其变为没有“共用点”的 a*a图便于我们运算。 那么a应该等于 （lcm（n-1，m-1））， 行放大倍数为a/n， 列放大倍数为a/m。

注意最后再加上1，因为“共用点总比边数少1”，换而言之就是有一条边是没有公共点的， 我们都按“lcm（n-1，m-1）”倍数去放大的话就会少算了一格。

这样我们就能得出“路径长”的公式为 lcm（n-1，m-1） + 1。

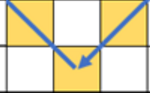
考虑2*3的格子， 现在行公用点其实是0， 格子共有3*1 = 3 个， 竖公共点有1个， 格子共有2+（2-1）*1 = 3 个。

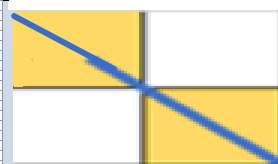
接下来我们处理，“路径长” 和“格子数”的关系。

由图可得， 因为有些格子走了2次（至多2次），所以"路径长”算多了一次。

其实 “路径长” =“走过一次格子数” * 1 + “走过两次格子数” * 2。

那么我们既然要求的是“走过一次的格子数”， 而且“路径长“也算出来了， 就可以得出。

"路径长" - “走过两次格子数”*2   =  “走过一次格子数” （即都视为走过两次的， 减掉路径就知道走过一次格子有多少）。

 

所以问题就转化为求“格子数”的问题了，

而且发现没有， 9 * 15的图中，按行算只有 4 ， 按列算只有7， 恰好是 lcm（8，14） = 56

56/ 8  = 7和  56 / 14 = 4 的结果。

这就说明， 我们用“共用点”计算的行列，是和我们放大的倍数有关系的。

那些走过两次的点， 其实就是行列的交叉点， 推了一下大概的公式，大概就是

#include<bits/stdc++.h>
using namespace std;
long long gcd(long long a, long long b){
    return b ==  ? a : gcd(b,a%b);
}
long long lcm(long long a, long long b){
    return a*b/gcd(a,b);
}
int main(){
    long long n , m;
    while(~scanf("%lld %lld", &n, &m)){
        long long l = lcm(n-,m-);
        long long a = l/(m-) , b = l/(n-);
        printf("%lld\n",l - a*b + a + b);
    }
    return ;
}