OpenCASCADE Gauss Integration

OpenCASCADE Gauss Integration

eryar@163.com

Abstract. Numerical integration is the approximate computation of an integral using numerical techniques. The numerical computation of an integral is sometimes called quadrature. The most straightforward numerical integration technique uses the Newton-Cotes formulas(also called quadrature formulas), which approximate a function tabulated sequence of regularly spaced intervals by various degree polynomials. If the functions are known analytically instead of being tabulated at equally spaced intervals, the best numerical method of integrations is called Gauss Integration(Gaussian quadrature). By picking the abscissas at which to evaluate the function, Gaussian quadrature produces the most accurate approximations possible. In OpenCASCADE math package it implement the Gauss-Legendre integration. So I will focus on the usage of the class in OpenCASCADE.

Key Words. OpenCASCADE, Gauss Integration, Gauss-Legendre, Numerical Analysis

1. Introduction

在科学和工程计算问题中，经常要计算一些定积分或微分，它们的精确值无法算出或计算量太大，只能用数值的方法给出具有指定误差限的近似值。最直观的数值积分方法有Newton-Cotes，其将积分区间等分之，并取分点为积分节点。这种做法虽然简化了计算，但却降低了所得公式的代数精度。

Gauss型求积公式是一种高精度的数值积分公式。在求积节点数相同的情况下，即计算工作量相近的情况下，利用Gauss型求积公式往往可以获得准确程序较高的积分结果，只是它在不等距的无理数上计算被积函数。

OpenCASCADE的math包中实现了Gauss-Legendre积分算法。本文主要介绍其使用方法，进而对其应用进行理解。

2. The Gauss-Legendre Integration

Gauss型求积公式是数值稳定的，且对有限闭区间上的连续函数，Gauss求积的数值随节点数目的增加而收敛到准确积分值。

常用的Gauss型求积公式有Gauss-Legendre求积公式，Gauss-Chebyshev求积公式，Gauss-Laguerre求积公式和Gauss-Hermite求积公式等。

对于一般区间[a, b]上的Gauss型求积公式，可通过变量变换，由Gauss-Legendre求积公式得到：

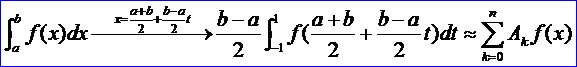其中：

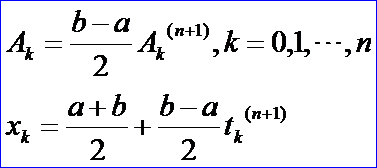
OpenCASCADE中对应的类有math_GaussSingleIntegration，主要实现的函数为Perform()，计算过程如下：

v 查表求得Gauss点及求积系数；

//Recuperation des points de Gauss dans le fichier GaussPoints.
  math::GaussPoints(Order,GaussP);
  math::GaussWeights(Order,GaussW);

v 根据Gauss-Legendre求积公式计算；

// Changement de variable pour la mise a l'echelle [Lower, Upper] :
  xm = 0.5*(Upper + Lower);
  xr = 0.5*(Upper - Lower);
  Val = .;

  Standard_Integer ind = Order/, ind1 = (Order+)/;
  if(ind1 > ind) { // odder case
    Ok1 = F.Value(xm, Val);
    if (!Ok1) return;
    Val *= GaussW(ind1);
  }
// Sommation sur tous les points de Gauss: avec utilisation de la symetrie.
  for (j = ; j <= ind; j++) {
    dx = xr*GaussP(j);
    Ok1 = F.Value(xm-dx, F1);
    if(!Ok1) return;
    Ok1 = F.Value(xm+dx, F2);
    if(!Ok1) return;
    // Multiplication par les poids de Gauss.
    Standard_Real FT = F1+F2;
    Val += GaussW(j)*FT;
  }
  // Mise a l'echelle de l'intervalle [Lower, Upper]
  Val *= xr;

对比Gauss-Legendre求积公式来理解上述代码还是比较清晰的。下面给出使用此类的一个具体实例：

/*
*    Copyright (c) 2014 eryar All Rights Reserved.
*
*        File    : Main.cpp
*        Author  : eryar@163.com
*        Date    : 2014-09-11 20:46
*        Version : 1.0v
*
*    Description : Demo for Gauss-Legendre Integration usage.
*
*      Key words : OpenCascade, Gauss-Legendre Integration
*/

#define WNT
#include <math_Function.hxx>
#include <math_GaussSingleIntegration.hxx>

#pragma comment(lib, "TKernel.lib")
#pragma comment(lib, "TKMath.lib")

class Test_GaussFunction : public math_Function
{
public:
    virtual Standard_Boolean Value(const Standard_Real x, Standard_Real &y)
    {
        y = x;

        return Standard_True;
    }

private:
};

void TestGaussIntegration(void)
{
    Test_GaussFunction aFunction;
    math_GaussSingleIntegration aSolver(aFunction, , , );

    std::cout << aSolver << std::endl;
}

int main(int argc, char* argv[])
{
    TestGaussIntegration();

    return ;
}

主要是从math_Function派生一个类来在虚函数Value()中重定义求积函数即可。上述实例中计算的是如下积分：

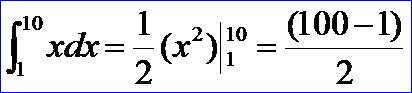
计算结果如下图所示：

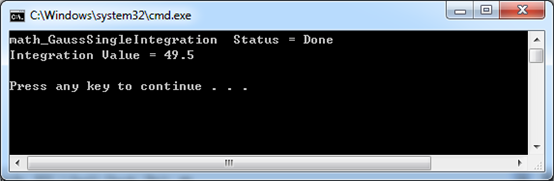
Figure 2.1 Gauss-Legendre Integtation Result

3. Application

由高等数学知识可知，积分的应用主要用于计算图形面积，体积及曲线的弧长，功等。

积分在OpenCASCADE中的主要应用有计算曲线长度，曲面面积及实体的体积等。如下图所示：

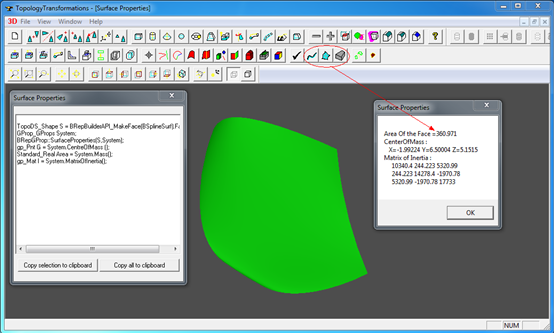
Figure 3.1 Compute Area of a Surface

示例代码如下所示：

TopoDS_Shape S = BRepBuilderAPI_MakeFace(BSS, Precision::Confusion()).Face();

GProp_GProps System;
BRepGProp::SurfaceProperties(S,System);
gp_Pnt G = System.CentreOfMass ();
Standard_Real Area = System.Mass();
gp_Mat I = System.MatrixOfInertia();

4. Conclusion

OpenCASCADE中实现的Gauss-Legendre求积算法，由于是查表求得Gauss点及求积系数，所以计算速度快。唯一不足是对高斯点数有限制。

综上所述，可知数值计算在OpenCASCADE中重要作用。一个TKMath库相当于实现了一本《数值分析》课本中的大部分内容。所以有兴趣的朋友可结合《数值分析》或《计算方法》之类的书籍，来对OpenCASCADE的数学库TKMath进行理论联系实际的深入理解。

5. References

1. Wolfram MathWorld, Numerical Integration,

http://mathworld.wolfram.com/NumericalIntegration.html

2. 易大义，沈云宝，李有法编. 计算方法. 浙江大学出版社. 2002

3. 易大义，陈道琦编. 数值分析引论. 浙江大学出版社. 1998

4. 李庆杨，王能超，易大义.数值分析.华中理工大学出版社. 1986

5. 同济大学数学教研室. 高等数学(第四版). 高等教育出版社. 1996

PDF Version: OpenCASCADE Gauss Integration