降维的作用：

  • 高维数据特征个数多，特征样本多，维度也很大，计算量就会很大，调参和最后评估任务时，计算量非常大，导致效率低。
  • 高位数据特征特别多，有的特征很重要，有的特征不重要，可以通过降维保留最好、最重要的特征。

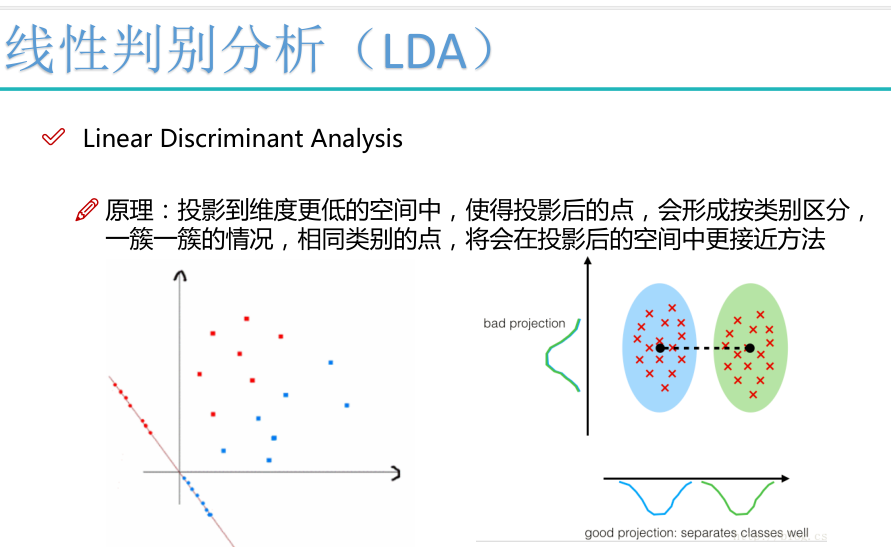
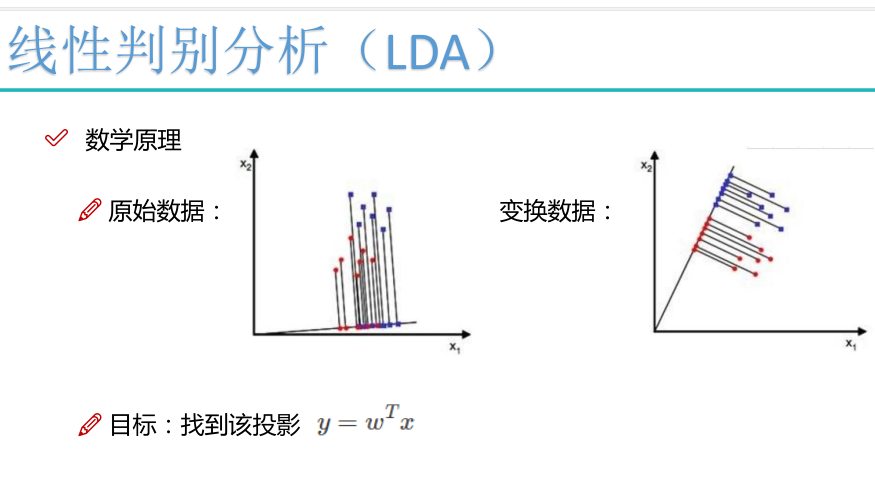
PCA是无类别信息，不知道样本属于哪个类，用PCA，通常对全体数据操作。
LDA有类别信息，投影到类内间距最小and类间间距最大...

注：类内散布矩阵：衡量映射后各自的密集程度。类间散布矩阵：衡量不同类别间的距离。

线性判别分析（LDA）的更多相关文章

  1. 机器学习 —— 基础整理（四）特征提取之线性方法：主成分分析PCA、独立成分分析ICA、线性判别分析LDA

    本文简单整理了以下内容: (一)维数灾难 (二)特征提取--线性方法 1. 主成分分析PCA 2. 独立成分分析ICA 3. 线性判别分析LDA (一)维数灾难(Curse of dimensiona ...

  2. 机器学习理论基础学习3.2--- Linear classification 线性分类之线性判别分析(LDA)

    在学习LDA之前,有必要将其自然语言处理领域的LDA区别开来,在自然语言处理领域, LDA是隐含狄利克雷分布(Latent Dirichlet Allocation,简称LDA),是一种处理文档的主题 ...

  3. 运用sklearn进行线性判别分析(LDA)代码实现

    基于sklearn的线性判别分析(LDA)代码实现 一.前言及回顾 本文记录使用sklearn库实现有监督的数据降维技术——线性判别分析(LDA).在上一篇LDA线性判别分析原理及python应用(葡 ...

  4. 线性判别分析LDA原理总结

    在主成分分析(PCA)原理总结中,我们对降维算法PCA做了总结.这里我们就对另外一种经典的降维方法线性判别分析(Linear Discriminant Analysis, 以下简称LDA)做一个总结. ...

  5. 线性判别分析LDA详解

    1 Linear Discriminant Analysis    相较于FLD(Fisher Linear Decriminant),LDA假设:1.样本数据服从正态分布,2.各类得协方差相等.虽然 ...

  6. 线性判别分析 LDA

    点到判决面的距离 点\(x_0\)到决策面\(g(x)= w^Tx+w_0\)的距离:\(r={g(x)\over \|w\|}\) 广义线性判别函数 因任何非线性函数都可以通过级数展开转化为多项式函 ...

  7. 机器学习中的数学-线性判别分析(LDA)

    前言在之前的一篇博客机器学习中的数学(7)——PCA的数学原理中深入讲解了,PCA的数学原理.谈到PCA就不得不谈LDA,他们就像是一对孪生兄弟,总是被人们放在一起学习,比较.这这篇博客中我们就来谈谈 ...

  8. 主成分分析(PCA)与线性判别分析(LDA)

    主成分分析 线性.非监督.全局的降维算法 PCA最大方差理论 出发点:在信号处理领域,信号具有较大方差,噪声具有较小方差 目标:最大化投影方差,让数据在主投影方向上方差最大 PCA的求解方法: 对样本 ...

  9. 线性判别分析（LDA）准则：FIsher准则、感知机准则、最小二乘（最小均方误差）准则

    准则 采用一种分类形式后,就要采用准则来衡量分类的效果,最好的结果一般出现在准则函数的极值点上,因此将分类器的设计问题转化为求准则函数极值问题,即求准则函数的参数,如线性分类器中的权值向量. 分类器设 ...

  10. LDA线性判别分析（转）

    线性判别分析LDA详解 1 Linear Discriminant Analysis    相较于FLD(Fisher Linear Decriminant),LDA假设:1.样本数据服从正态分布,2 ...

随机推荐

  1. WaveNet: 原始音频生成模型

    官方博客 WaveNet: A Generative Model for Raw Audio paper地址:paper Abstract WaveNet是probabilistic and auto ...

  2. iOS开发检测是否开启定位、是否允许消息推送等权限

    1.iOS开发检测是否开启定位: 需要导入: #import <CoreLocation/CoreLocation.h> 代码如下: + (void)openLocationService ...

  3. Codeforces630C【水题】

    题意: 有一种数只会有7或者8构成,给一个n,问你前n位上有多少个这样的数. 思路: 对于一个 i 位,有2^i个数,然后前n项和就是2^(n+1)-2; 复习一下等比数列求和,等差数列求和吧; ①: ...

  4. 转载文章 -- 难搞的滚动事件(滚动默认，scrollTop)

    关于取消默认事件 现今的 chrome 浏览器,为了实现丝滑顺畅地滑动,活动时间直接执行而不再检测默认事件,这使得无法用 e.preventDafult() 来阻止默认事件. 现在需要添加 {pass ...

  5. 莫队初探（不带修/例题极少）By cellur925

    因为今天考到莫队裸题了嘤嘤嘤...而我这样的蒟蒻肯定不会这样的高端算法啊QAQ.于是暴力水了40分qwq. 正如上文所说,我实在太菜了,于是学习莫队也只是学习了最简单的不带修普通莫队,如果我能苟到省选 ...

  6. _bzoj1911 [Apio2010]特别行动队【斜率优化dp】

    传送门:http://www.lydsy.com/JudgeOnline/problem.php?id=1911 裸的斜率优化dp. #include <cstdio> const int ...

  7. 转 python 将一个文件中内容添加到另一个文件指定位置

    http://blog.csdn.net/huguangshanse00/article/details/14624601

  8. E. Anton and Tree 数组开大点

    http://codeforces.com/contest/734/problem/E 看了题解,缩点 + 树的直径. 然而一直wa14. 注意到, 缩点后重建图,在5的时候,5和6建了一条边,然后6 ...

  9. PV,UV,IP概念

    PV是网站分析的一个术语,用以衡量网站用户访问的网页的数量.对于广告主,PV值可预期它可以带来多少广告收入.一般来说,PV与来访者的数量成正比,但是PV并不直接决定页面的真实来访者数量,如同一个来访者 ...

  10. Unity3D中GameObject 详细介绍

    通过Hierarchy面板下的Create菜单可以手动地创建一个GameObject,它可以是一个相机,一个灯光,或者一个简单的模型,当我们要在程序里面动态地创建一个相机的时候,可以new一个Game ...