滑动窗口的最大值 · sliding-window-maximum

［抄题］：

Given an array nums, there is a sliding window of size k which is moving from the very left of the array to the very right. You can only see the k numbers in the window. Each time the sliding window moves right by one position.

For example,
Given nums = [1,3,-1,-3,5,3,6,7], and k = 3.

Window position                Max
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

Therefore, return the max sliding window as [3,3,5,5,6,7].

[暴力解法]：

时间分析：

空间分析：

［思维问题］：

［一句话思路］：

左边括号移动挤掉大的，右边挤掉小的。所以两边都要开口，用deque（递减队列）

［输入量］：空： 正常情况：特大：特小：程序里处理到的特殊情况：异常情况（不合法不合理的输入）：

［画图］：

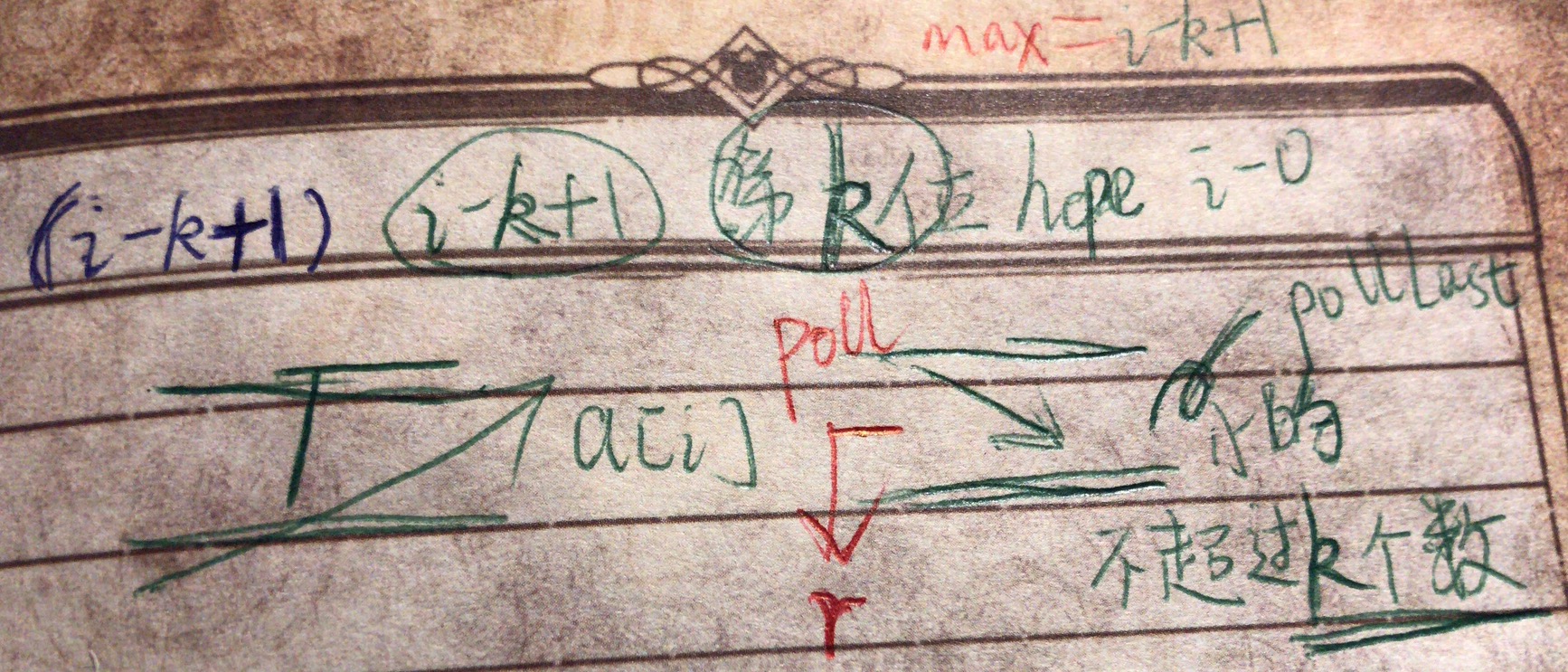
［一刷］：

1. return result是利用第二次，初始化为0了。return new int[0]是利用第一次，里面没东西。
2. 类似于heap，deque取最大值都是用peek（）

［二刷］：

［三刷］：

［四刷］：

［五刷］：

[五分钟肉眼debug的结果]：

［总结］：

取最大值都要用peek（）

［复杂度］：Time complexity: O(并非每个元素都要一进一出，<2n) Space complexity: O(n)

［英文数据结构或算法，为什么不用别的数据结构或算法］：

deque的实现是arraydeque

［关键模板化代码］：

［其他解法］：

［Follow Up］：

［LC给出的题目变变变］：

76. Minimum Window Substring 哈希表，还挺复杂

[代码风格] ：

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        //corner case
        int[] result = new int[nums.length - k + 1];
        int index = 0;
        if (nums == null || k <= 0) {
            return new int[0];
        }
        Deque<Integer> q = new ArrayDeque<Integer>();

        for (int i = 0; i < nums.length; i++) {
            //get nums out of range k
            while (!q.isEmpty() && i - k + 1 > q.peek()) {
                q.poll();
            }
            //get nums smaller
            while (!q.isEmpty() && nums[i] > nums[q.peekLast()]) {
                q.pollLast();
            }
            //get nums bigger, add to result
            q.offer(i);
            if (i >= k - 1) {
                result[index++] = nums[q.peek()];
            }
        }

        return result;
    }
}