JSOI BZOJ4472 salesman

题目大意

某售货员小T要到若干城镇去推销商品,由于该地区是交通不便的山区，任意两个城镇
之间都只有唯一的可能经过其它城镇的路线。小T 可以准确地估计出在每个城镇停留的净收
益。这些净收益可能是负数，即推销商品的利润抵不上花费。由于交通不便，小T经过每个
城镇都需要停留，在每个城镇的停留次数与在该地的净收益无关，因为很多费用不是计次收
取的，而每个城镇对小T的商品需求也是相对固定的，停留一次后就饱和了。每个城镇为了
强化治安，对外地人的最多停留次数有严格的规定。请你帮小T 设计一个收益最大的巡回方
案,即从家乡出发，在经过的每个城镇停留，最后回到家乡的旅行方案。你的程序只需输出
最大收益，以及最优方案是否唯一。方案并不包括路线的细节，方案相同的标准是选择经过
并停留的城镇是否相同。因为取消巡回也是一种方案，因此最大收益不会是负数。小T 在家
乡净收益是零，因为在家乡是本地人，家乡对小 T当然没有停留次数的限制。

输入

输入的第一行是一个正整数ｎ(5<=n<=100000)，表示城镇数目。城镇以１到ｎ的数命名。小T 的家乡命
名为１。第二行和第三行都包含以空格隔开的ｎ－１个整数，第二行的第ｉ个数表示在城镇
ｉ＋１停留的净收益。第三行的第ｉ个数表示城镇ｉ＋１规定的最大停留次数。所有的最大
停留次数都不小于２。接下来的ｎ－１行每行两个１到ｎ的正整数ｘ，ｙ，之间以一个空格
隔开，表示ｘ，ｙ之间有一条不经过其它城镇的双向道路。输入数据保证所有城镇是连通的。

输出

输出有两行，第一行包含一个自然数，表示巡回旅行的最大收益。如果该方案唯一，在
第二行输出“solution is unique”，否则在第二行输出“solution is not unique”。

样例

样例输入

- -   -

样例输出

solution is unique

//最佳路线包括城镇 1，2， 4， 5， 9。

分析

题目中的任意两个城镇之间都只有唯一的可能经过其它城镇的路线非常重要，这就说明题目中给出的图一定是一棵树

因此，联系最近学过的内容，我们可以用树形DP求解

题目中给出了停留次数的限制，这其实就是给出了你最多能访问多少子树

注意：在一个节点停留n次说明你可以遍历n-1棵子树，因为你还要从子树返回这一个节点，所以在读入时要w--（为了方便，后文的停留次数都是指--之后的）

那么动态转移方程是什么呢？

其实很简单，就是在停留次数限制内选择价值最大的子树，同时如果一个子树的价值为负，那么我们就不能选

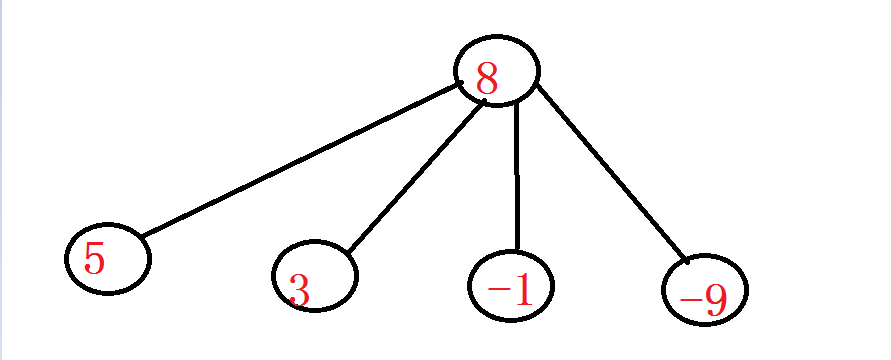
比如上面这幅图，如果在父亲节点只能停留1次，则我们要选择价值最大的节点5

如果停留2次，我们要选择价值最大的两个节点5、3

如果停留3次呢，我们是选择5、3、-1吗？显然不是，因为选择-1这个点会拉低价值，所以我们只选5、3两个点就可以

知道了怎么选择节点，我们来看一下什么情况会出现多种选择

1、既然是重复，那么两个节点价值相同的情况一定要考虑一下

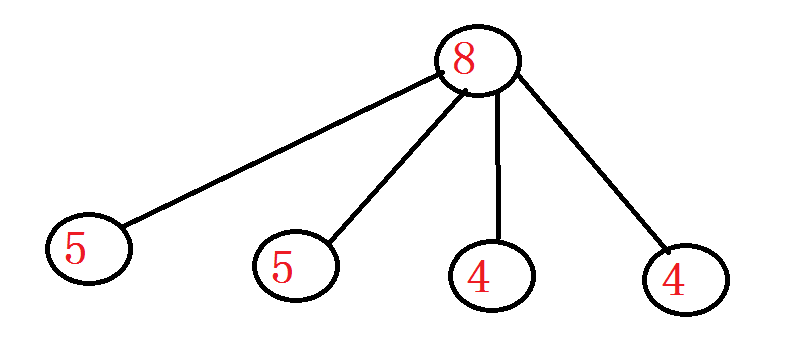
我们看上面这幅图

如果在父亲节点只能停留1次，则我们会有两种情况：选左边的5或者右边的5

如果停留2次，我们只有一种情况：两个5都选

如果停留3次，我们也有两种情况：选上2个5，左边的4和右边的4再任选一个

停留4次呢？又只有一种了

所以，只有当父亲节点剩余的停留次数为1，而且此时最大值有两个及以上儿子节点，那么就会有多种情况

2、子节点的价值为零

这种情况比较特殊，因为无论你选没选到他，价值都是一样，所以会有两种选择

但是前提是价值为0的节点必须前k大的节点之内，因为如果你都遍历不到他，更谈不上决策了

记录子节点的最大值我们用优先队列就可以

代码

把这两种情况搞清之后，我们就可以开始写代码了

代码的细节在注释里

 #include<cstdio>

 #include<cstring>

 #include<algorithm>

 #include<iostream>

 #include<cmath>

 #include<queue>

 using namespace std;

 const int maxn=2e5+;

 struct asd{

     int from,to,next;

 }b[maxn];

 int tot=,head[maxn];

 int da[maxn],cx[maxn];

 void ad(int aa,int bb){

     b[tot].from=aa;

     b[tot].to=bb;

     b[tot].next=head[aa];

     head[aa]=tot++;

 }//建边

 int f[maxn];//记录最大值

 int jud;

 void dfs(int now,int fa){

     priority_queue<int> q;//默认大根堆

     for(int i=head[now];i!=-;i=b[i].next){

         int u=b[i].to;

         if(u==fa) continue;

         dfs(u,now);

         q.push(f[u]);//遍历，同时将子节点的值pop进去

     }

     int cnt=,jl=0x3f3f3f3f;

     if(q.size()>=){

         int xx=q.top();

         q.pop();

         jl=q.top();

         q.push(xx);

     }

     //cnt记录所选元素的个数，jl记录上一次选的元素

     //这道题数据很水，把jl赋值成0x3f3f3f3f都能过

     //下面是错误写法

     /*

     int cnt=0,jl=0x3f3f3f3f;或者jl=0;jl=任何数

     没有后面的判断

     虽然能过，但是不对

     */

     while(!q.empty()){

         cnt++;

         int xx=q.top();

         if(xx== || (cx[now]==cnt && jl==xx)){

             jud=;

         }//有两种决策的情况

         if(xx< || cx[now]+==cnt) break;//超过停留次数

         f[now]+=xx;

         jl=xx;

         q.pop();//一定要pop

     }

     while(!q.empty()) q.pop();//pop不pop都可以

 }

 int main(){

     memset(head,-,sizeof(head));

     int n;

     scanf("%d",&n);

     for(int i=;i<=n;i++){

         scanf("%d",&da[i]);

     }

     for(int i=;i<=n;i++){

         scanf("%d",&cx[i]);

         cx[i]--;//一定要--

     }

     cx[]=0x3f3f3f3f;//1号节点可以停留无数次

     for(int i=;i<=n;i++){

         int aa,bb;

         scanf("%d%d",&aa,&bb);

         ad(aa,bb);

         ad(bb,aa);//建边

     }

     for(int i=;i<=n;i++){

         f[i]=da[i];//给每一个节点初始化价值

     }

     dfs(,);//从根节点开始遍历

     if(jud) printf("%d\nsolution is not unique\n",f[]);

     //有多种情况也要输出值，不要忘了

     else printf("%d\nsolution is unique\n",f[]);

     return ;

 }

这道题思维量不小，大家一定要认真思考