Skip Lists: A Probabilistic Alternative to Balanced Trees 阅读笔记

论文地址：https://15721.courses.cs.cmu.edu/spring2018/papers/08-oltpindexes1/pugh-skiplists-cacm1990.pdf

关键点：

1、在算法内部引入随机性，从而避免对插入顺序随机性的依赖

2、如何插入和删除一个元素，同时更新前驱节点的第k跳指针

3、如何为一个新增的node分配一个合适的level

4、MaxLevel应该选多少

综述

跳表使用一种概率上的平衡而非强制平衡（相较于balance tree），使得插入和删除操作比同类的平衡算法（balance tree）更低。

前言

binary tree可用于表示抽象的数据结构，例如字典、有序列表等。当元素为按随机顺序插入时，binary tree可以很好的工作，但当元素按顺序插入时，性能急剧退化。如果在插入前，可以对插入的元素进行随机化排序，那么就可以使得binary tree拥有良好的性能。但是由于binary tree通常需要在线响应动作（In most cases queries must be answered on-line），因此提前将待插入元素随机化是不切实际的。balance tree算法会在执行树的操作时，re-arange树的形状，使得树始终保持某种平衡规则（例如左子树与右子树高度之差不超过1），以保持树的检索性能。

跳表是平衡树的一种概率替代方案。

跳表通过咨询（consulting？？）一个随机数生成器来实现平衡。（Skip lists have balance properties similar to that of search trees built by random insertions, yet do not require insertions to be random.）

（既然不能保证insert的顺序是随机的，那么就在算法内部引入一个随机来达到保持平衡的效果）

SKIP LISTS

当搜索一个linked list时，我们需要遍历这个linked list中的每个元素。时间复杂度O(N)。

若链表是有序的，并且每个node上都保存了到达下两跳节点的指针（has a pointer to the node two ahead it in the list），那么我们最多只需要搜索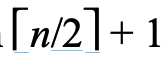个节点。

同理，若我们保存了下四跳的节点，那么需要搜索的节点数就减少至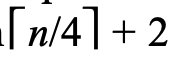个。

若每第个节点，都有指向第跳节点的指针，那么在linked list中查找元素时需要检索的节点数量将减少至个，而指针的数量只翻了一倍。这样的数据结结构将拥有高效的搜索速度，但是对这样的数据结构进行插入或删除操作几乎是不切实际的（因为每插入或删除一个元素，都需要重新调整下x跳指针指向的node）。一个节点若包含若指向下K个节点的指针，则我们称它为level K node。如果每第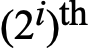个节点都包含后续第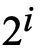个节点的指针，则每类levels节点的比率分布是固定的：

50%的节点包含level 1，25%的节点包含level 2，12.5%的节点包含level 3，以此类推。

若每个节点的level是随机生成的（但每层的节点概率仍然按照上述比例50%、25%、12.5%...进行分配），会发生什么事情呢？

SKIP LIST ALGORITHMS

这一章节会介绍算法的搜索、插入和删除操作。

搜索：返回某个key对应的value，若key不存在则返回fail。

插入：将制定的key与new value对应起来（若key尚不存在，则新增一个node）。

删除：删除制定的key。（疑问：删除一个node时，如何更新指向这个node的前置节点的level pointer???）

诸如“查找最小key”、“查找下一个key”等额外操作都很容易实现。

跳表中的每一个元素，都用一个node来表示。每个node的层数都是随机生成的，不依赖于当前结构中包含的元素个数。（Each element is represented by a node, the level of which is chosen randomly when the node is inserted without regard for the number of elements in the data structure. ）

初始化（Initialization）

初始化一个list，下一跳为nil，当前最大level为1。

搜索算法（Search Algorithm）

按当前节点的leve高pointer向level1 pointer搜索，若forward[i].key < searchKey，则换forward[I]的node继续尝试，直到找到（return value）或找不到（fail）时返回。

插入和删除算法（Insertion and Deletion Algorithms）

在执行插入和删除操作时，算法只是执行简单的搜索和拼接动作。例如：

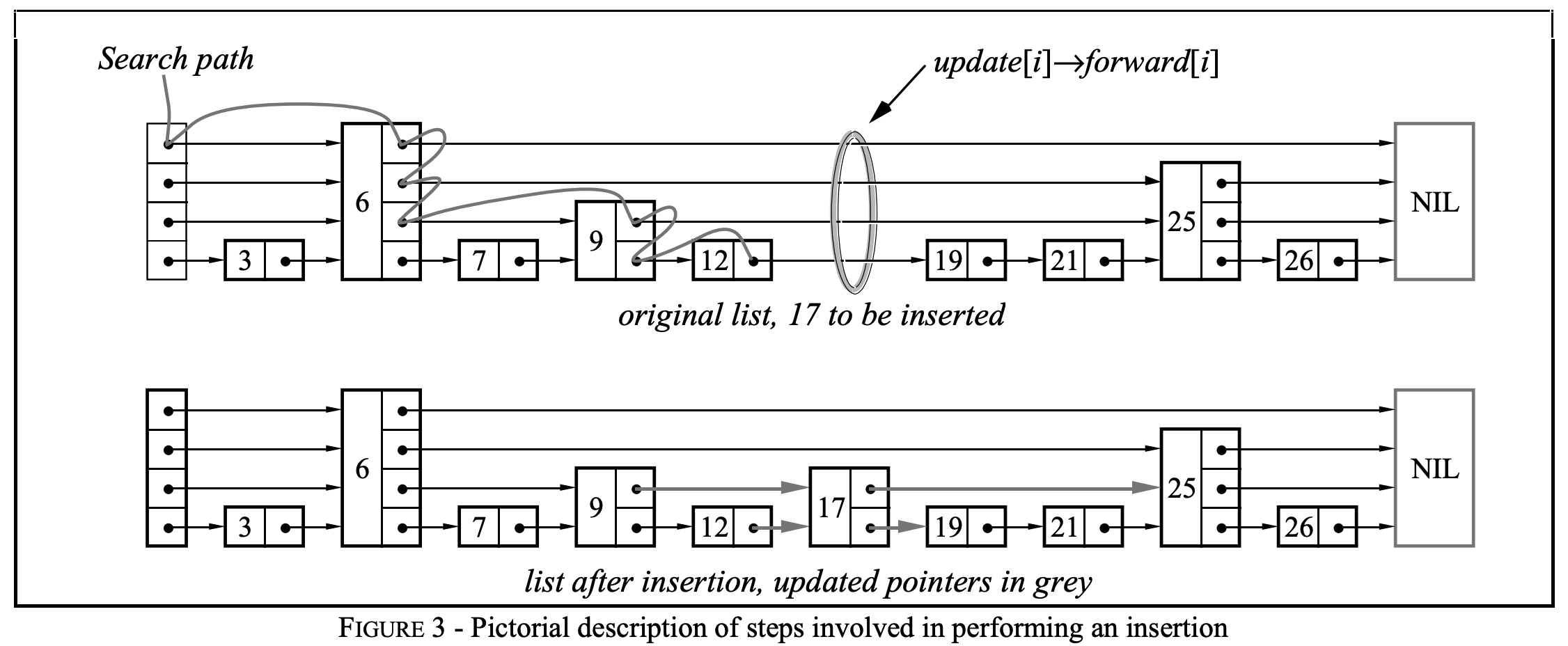
插入算法

（1）从skip list的header开始，先搜索到比searchKey小的最靠右的node，并存储在update[i]中（i表示层数）

如上图实例中，在完成search时，update中的值为:

update[LEVLE4] = node6

update[LEVEL3] = node6

update[LEVEL2] = node9

update[LEVEL1] = node12

（2）判断node->forward[1]的key是否等于searchKey，若等于则说明key已经存在，则直接更新value=newValue后即可返回;否则，进入(3)

（3）新增一个node，过程如下：

（a）随机生成一个level  lvl（但概率还是按照上文提到的比率），若新lvl比现有的最大level高，则执行(a.1)(a.2)

（a.1）将update[currLevel]到update[lvl]数组元素的值都更新为list->header

（a.2）更新list->level为这个新生成的lvl。

（b）new一个新的node X，入参为lvl、searchKey、value

（c）更新node X各level的指针

(c.1) X->forward[i] = update[i]->forward[i]

此时，按上述例子，各个节点的forward信息更新为（因为node17随机生成到的level是2，所以只会有level2和level1的forward指针）

node17->forward[LEVEL2] = update[LEVEL2]->forward[LEVEL2] = node9->forward[LEVEL2] = node25

node17->forward[LEVEL1] = update[LEVEL1]->forward[LEVEL1] = node12->forward[LEVEL1] = node19

(c.2) update[I]->forward[i] = X

此时，按上述例子

update[LEVEL2] = node9,  node9->forward[LEVEL2] = node17

update[LEVEL1] = node12,  node12->forward[LEVEL1] = node17

插入算法伪代码

删除算法

（1）如同上述插入算法，也是先检索到searchKey所在的NodeX，并且在检索过程中，生成一个udpate[i]向量

（2）对于level 1 -》K （K为当前跳表中最大的有效层数）

(a) 若update[level i]->forward[level i] == nodeX,  则update[level i]->forward[level i] = x->forward[level i];

(b) 若update[level i]->forward[level i] != nodeX,  则 break循环。（因为update[level i]->forward[level i]不为nodeX，说明NodeX的level层数不够高，update[level i]->forward[level i]指向了nodeX之后的其他节点，因此可以break了）

（3）free nodeX

（4）遍历list->level到1，若list->header->forward[level i] == NIL了，则将list->level减一

例如，想要删除node17，那么：

（1）完成search操作后的update向量为

update[4] = node6

update[3] = node6

update[2] = node9

update[1] = node12

(2) 遍历更新前向节点的下k跳节点

update[1] = node12, node12->forward[1] = node17->forward[1] = node19

update[2] = node9, node9->forward[2] = node17->forward[2] = node25

update[3] = node6, node6->forward[3] = node25 > node 17, break

(3) free node17

(4) 因为node17的level只有2，所以不会导致List->level的变化

我们再尝试删除一下node6，过程为：

（1）完成search操作后的update向量为

update[4] = list->header

update[3] = list->header

update[2] = list->header

update[1] = node3

(2) 遍历更新前向节点的下k跳节点

update[1] = node3, node3->forward[1] = node6->forward[1] = node7

update[2] = list->header, list->header->forward[2] = node6->forward[2] = node9

update[3] = list->header, list->header->forward[3] = node6->forward[3] = node25

update[4] = list->header, list->header->forward[4] = node6->forward[4] = NIL, break

(3) free node6

(4) 更新list->level

此时，list->level == 4

for i:= 4 to 1

list->header[4] == NIL, list->level = 4-1 = 3

list->header[3] == node25, break

此时，list->level == 3

删除算法伪代码

选择一个随机level （Choosing a Random Level）

计算随机level的伪代码（按上述例子，p=1/2）

因为p=1/2，所以我们可以用抛硬币的场景来模拟一下。

lvl的初始值是1，而想让lvl+1的条件是我必须能random到一个小于0.5的值（假设为抛到硬币的正面吧）

那么，若我希望lvl == 2，则意味着我必须两次抛到硬币的正面才行，那么概率就是0.5*0.5

若我希望lvl == 3， 则必须连续三次抛到硬币的正面，则概率为 0.5*0.5*0.5

依次类推，若希望得到更高的lvl，则需要连续抛到正面的次数要求越多，概率也随之降低。

应该从第几层检索（At what level do we start a search? Defining L(n)）

按照刚刚的随机level生成器，对于一个有16个节点的linked list，我们可能得到这样的结果

level1 有9个节点

level2 有3个节点

level3 有3个节点

level14 有1个节点   （概率非常非常低，需要连续13次抛出硬币的正面）

若我们每次搜索都从level 14开始，那么会有很多无用功。（因为level 4-13都是只有一个节点）。

那么，我们应该从哪个level开始做搜索呢？

理想情况下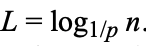，为下文描述方便此公式简写为L(n)

当list中有一个元素拥有异常巨大的level时，我们通常有如下几种应对方法.

策略一： Don’t worry, be happy.

就按list->level来搜索，某个节点的level远远大于L(n)的概率是极地极低的。

策略二：  Use less than you are given.

尽管对于level14的node，我们有14个forward指针，但是可以将其优化到仅使用L(n)个指针。不过这个优化的成本很高，但收益很小，因此不推荐用这种方法。

策略三：Fix the dice

把筛子固定下来，对于每个newNode，都简单粗暴的将它的level定义为当前最大level+1。

但是这样会导致算法的随机性被打破。

（那能否每次随机生成level时，maxLevel等于当前最大有效level+1呢？这样一来，可以缓慢的趋近预设的MAXLevel，而不至于中间出现很多断层的level）

MaxLevel取多少合适（Determining MaxLevel）

直接给结论吧

MaxLevel = L(N) (where N is an upper bound on the number of elements in a skip list).

对于p=1/2 , MaxLevel = 16的跳表，可以存储2¹⁶个元素。