统计决策——贝叶斯决策理论（Bayesian Decision Theory）

（本文为原创学习笔记，主要参考《模式识别（第三版）》（张学工著，清华大学出版社出版））

1.概念

将分类看做决策，进行贝叶斯决策时考虑各类的先验概率和类条件概率，也即后验概率。考虑先验概率意味着对样本总体的认识，考虑类条件概率是对每一类中某个特征出现频率的认识。由此不难发现，贝叶斯决策的理论依据就是贝叶斯公式。

2.理论依据

2.1 最小错误率贝叶斯决策

贝叶斯决策的基本理论依据就是贝叶斯公式（式1），由总体密度P(E)、先验概率P(H)和类条件概率P(E|H)计算出后验概率P(H|E)，判决遵从最大后验概率。这种仅根据后验概率作决策的方式称为最小错误率贝叶斯决策，可以从理论上证明这种决策的平均错误率是最低的。另一种方式是考虑决策风险，加入了损失函数，称为最小风险贝叶斯决策。

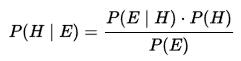   ……（式1）

【证明】最小错误率贝叶斯决策的平均错误率最低

以二分类问题为例，对于样本x的决策错误率如式2：

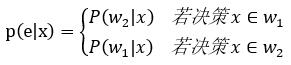……（式2）

更进一步得到式3：

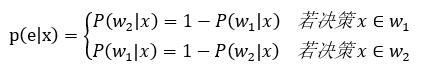……（式3）

将决策的错误率看做服从同样分布的样本的理论错误率的期望，也即：

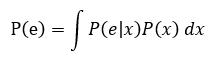……（式4）

通过式3和式4得出，最小错误率意味着每一个决策都必须遵从最大后验概率。而最小错误率贝叶斯决策的判决方式就是遵从最大后验概率。

【证明完毕】

2.2 最小风险贝叶斯决策

前文论述了最小错误率贝叶斯决策的理论依据，并且证明了最小错误率的由来。接下来说明最小风险贝叶斯决策的理论依据。

决策往往意味着风险，这是实际决策中的常见情形。在做出风险性决策时尤为需要考虑风险，比如巨额投资的决策，如果采取激进策略可能会带来巨额损失，而保守策略就不会有风险。各种决策的风险可以用决策表表示，如表1。假设ω₁表示亏损，α₁表示保守决策；ω₂表示盈利，α₂表示激进决策。如果预测对了自然不会带来风险，但是如果做出了激进决策，可是接下来却是亏损状态，那这个决策具有较大的风险，因此给定风险值5；而在做出保守决策后出现盈利状态也会带来一定的风险，但不至于亏损本金，因此给定风险值1。

（表1 决策表）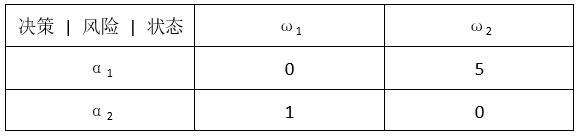

为了实现最小风险贝叶斯决策，在判决函数中加入损失函数（式5）。

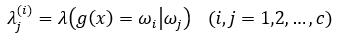……（式5）

式5表示将j类误判为i类的损失，c为类数。由λ构成一个c×c的损失矩阵，也即表示决策表。

最小风险贝叶斯决策的判决函数为：

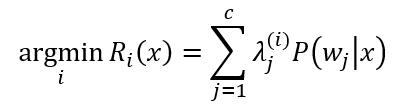……（式6）

3.贝叶斯决策的一般过程

（1）估计先验概率：①根据实际情况做经验估计；②根据样本分布的频率估计概率。

（2）计算类条件概率密度：①参数估计：类条件概率分布类型已知，参数未知，通过训练样本来估计（最大似然法、Bayes估计）；②非参数估计：不判断类条件概率分布类型，直接根据训练样本来估计（Parzen窗、k_n-近邻法）。

（3）计算后验概率。

（4-1）若进行最小错误率决策，根据后验概率即可作出决策。

（4-2）若进行最小风险决策，按照式6计算即可。

4. ROC曲线

ROC曲线全称为受试者工作特征曲线 （receiver operating characteristic curve），以特异度为横轴、敏感度为纵轴绘制，用来评价一种分类方法或者评价多种分类方法的优劣，越贴近左上角，则这种分类方法性能越好。

5. MATLAB实现一维二分类最小错误率贝叶斯决策

具体编程实现时，只需要按照3中的贝叶斯决策的一般过程就能实现。我在实现时采用样本的频率估计先验概率，采用高斯分布假设、最大似然法估计参数确定类条件概率密度。数据是来自班上男女同学的身高，实现根据身高判断性别。直接贴图。

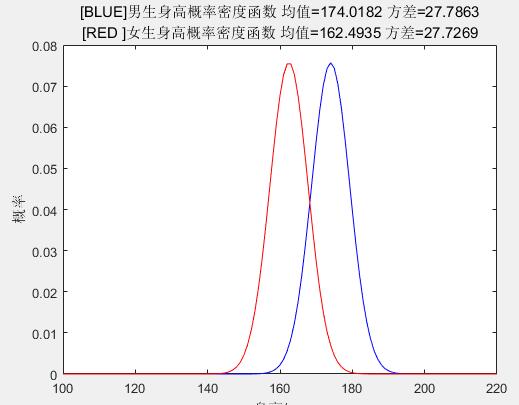
（图1 一维二分类最小错误率贝叶斯决策类条件概率密度曲线）

（图2 一维二分类最小错误率贝叶斯决策实验输出）

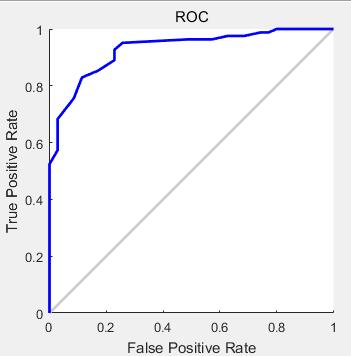
（图3 一维二分类最小错误率贝叶斯决策ROC曲线）

6. MATLAB实现二维二分类最小错误率贝叶斯决策

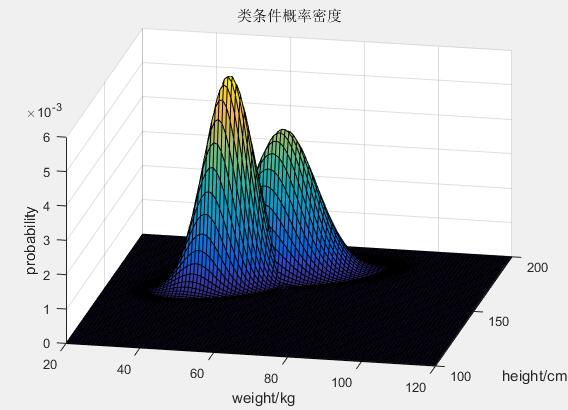
（图4 二维二分类最小错误率贝叶斯决策类条件概率密度）

（图5 二维二分类最小错误率贝叶斯决策实验输出）

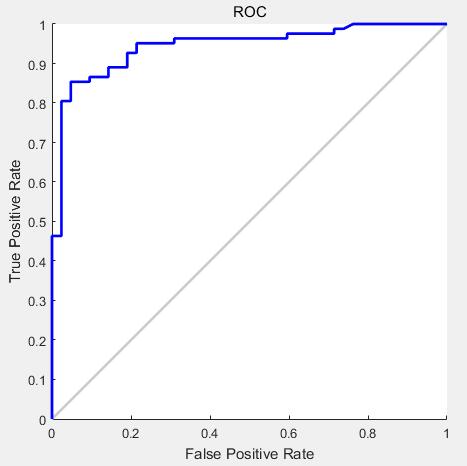
（图6 二维二分类最小错误率贝叶斯决策ROC曲线）

7. MATLAB实现一维二分类最小错误率贝叶斯决策（使用Parzen窗非参数估计确定类条件概率密度）

比较图7和图1可以看出，由参数估计方法得到的类条件概率密度曲线是光滑的高斯分布，而Parzen窗非参数估计方法得到的类条件概率密度曲线是并不光滑，但是也接近于高斯分布，由此也可以看出大数定理是有道理的。

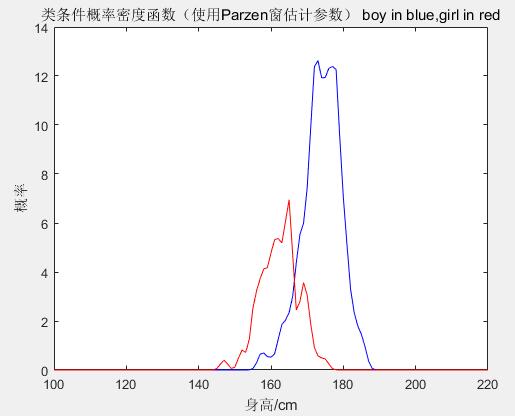
（图7 一维二分类最小错误率贝叶斯决策（使用Parzen窗非参数估计确定类条件概率密度）类条件概率密度）

（图8 一维二分类最小错误率贝叶斯决策（使用Parzen窗非参数估计确定类条件概率密度）实验输出）

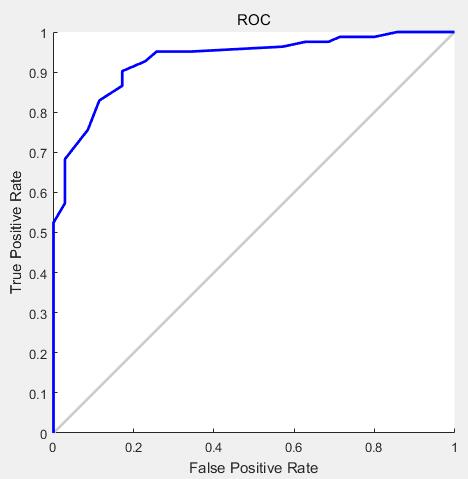
（图9 一维二分类最小错误率贝叶斯决策（使用Parzen窗非参数估计确定类条件概率密度）ROC曲线）

8. MATLAB实现二维二分类最小风险贝叶斯决策

为了防止把男同胞误认为女生，我设置了如图表10所示的决策表，把男生判为女生的风险为5，女生判为男生的风险为1。

注意观察比较图12和图5，对于同样的测试样本集，在考虑最小风险时没有男生被误判，但是女生的错误率明显升高，这就是最小错误率和最小风险的区别。

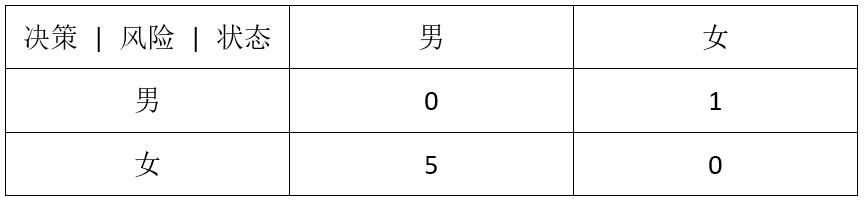
（图10 二维二分类最小风险贝叶斯决策的决策表）

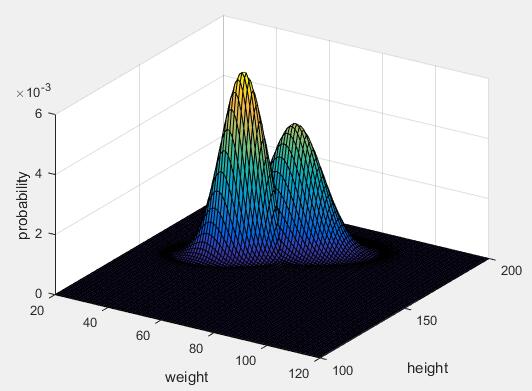
（图11 二维二分类最小风险贝叶斯决策类条件概率密度）

（图12 二维二分类最小风险贝叶斯决策实验输出）

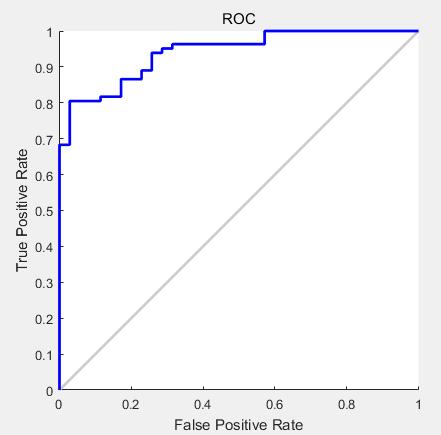
（图13 二维二分类最小风险贝叶斯决策ROC曲线）

9. 致谢

以上内容根据上海大学计算机工程与科学学院《模式识别》课程实验内容整理而成，相关理论参考了张学工著《模式识别（第三版）》。在此尤为感谢方昱春老师的授课与实验指导！同时感谢段同学对于某函数参数的帮助！