凸包（Convex Hull）构造算法——Graham扫描法

凸包（Convex Hull）

在图形学中，凸包是一个非常重要的概念。简明的说，在平面中给出N个点，找出一个由其中某些点作为顶点组成的凸多边形，恰好能围住所有的N个点。

这十分像是在一块木板上钉了N个钉子，然后用一根绷紧的橡皮筋它们都圈起来，这根橡皮筋的形状就是所谓的凸包。

计算凸包的一个著名算法是Graham Scan法，它的时间复杂度与所采用的排序算法时间复杂度相同，通常采用线性对数算法，因此为\( O\left(N\mathrm{log}\left(N\right)\right) \)。

1. 找到所有点\( P_{0,1,...,N-1} \)中最下方的点，记为\( P_{L} \)；

2. 计算所有其他的点\( P_{i}\left(i\neq L\right) \) 与 \( P_{L} \)构成的向量\( \overrightarrow{P_{L}P_{i}} \)相对于水平轴的夹角。因为所有的点都在该\( P_{L} \)上方，因此向量的取值范围为\( \left(0, 180\right) \) ，所以可以用余切值代替角度值；

3. 对所有其他的点按照第2步算出的角度进行排序，且\( P_{L} \)为排序后的数组的第0位；

4. 从点\( P_{L} \)开始，依此连接每一个点（已经排序过），每连接一个点检测连线的走向是否是逆时针的，如果是则留下该点的前一个点，反之去除前一个点，使之与前面第二个点直接连接，继续这一检测，直到是逆时针或者所有点都被检测过为止。

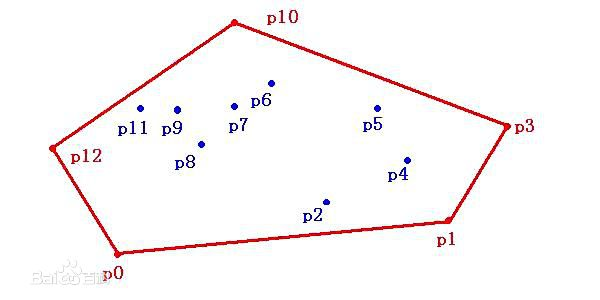
判断三个点依此连成两条线段走向是否为逆时针，用这两条线段向量的叉积判断：叉积>0，逆时针；反之顺时针或者共线。

这里采用Qt 5.7实现了一个算法的演示程序，其中算法的部分如下（由于在Qt的坐标系中，y向下增长，因此在计算纵坐标差值时需要取相反数）。

void DisplayWidget::calConvexHull()
{
    int size = m_points.size();
    if (size < )
    {
        return;
    }

    // First: find the lowest point
    int maxY = ;
    int indexOfLowest = -;
    for (int i = ; i < size; i++)
    {
        if (m_points.at(i).y() > maxY)
        {
            maxY = m_points.at(i).y();
            indexOfLowest = i;
        }
    }

    std::swap(*m_points.begin(), *(m_points.begin() + indexOfLowest));
    QPoint &lowestPoint = *(m_points.begin());

    // Second: calculate ctan(angles)
    double *ctanAngles = new double[size];
    for (int i = ; i < size; i++)
    {
        double deltaY = lowestPoint.y() - m_points.at(i).y() + DBL_EPSILON;
        double deltaX = m_points.at(i).x() - lowestPoint.x();
        ctanAngles[i] = deltaX / deltaY;
    }

    // Third: Sort subscript
    int *subscript = new int[size];
    for (int i = ; i < size; i++)
    {
        subscript[i] = i;
    }
    std::sort(subscript + , subscript + size, [ctanAngles](int a1, int a2) { return ctanAngles[a2] < ctanAngles[a1]; });

    // Fourth: Calculate convex hull
    std::vector<QPoint> convexHullPoints;
    convexHullPoints.push_back(*m_points.begin());
    convexHullPoints.push_back(m_points.at(subscript[]));

    for (int i = ; i < size; i++)
    {
        convexHullPoints.push_back(m_points.at(subscript[i]));
        while (convexHullPoints.size() >  &&
               !isAnticlockwise(*(convexHullPoints.end() - ), *(convexHullPoints.end() - ), *(convexHullPoints.end() - )))
        {
            *(convexHullPoints.end() - ) = *(convexHullPoints.end() - );
            convexHullPoints.pop_back();
        }
    }

    m_convexHullPoints = std::move(convexHullPoints);

    delete[] ctanAngles;
    delete[] subscript;
}

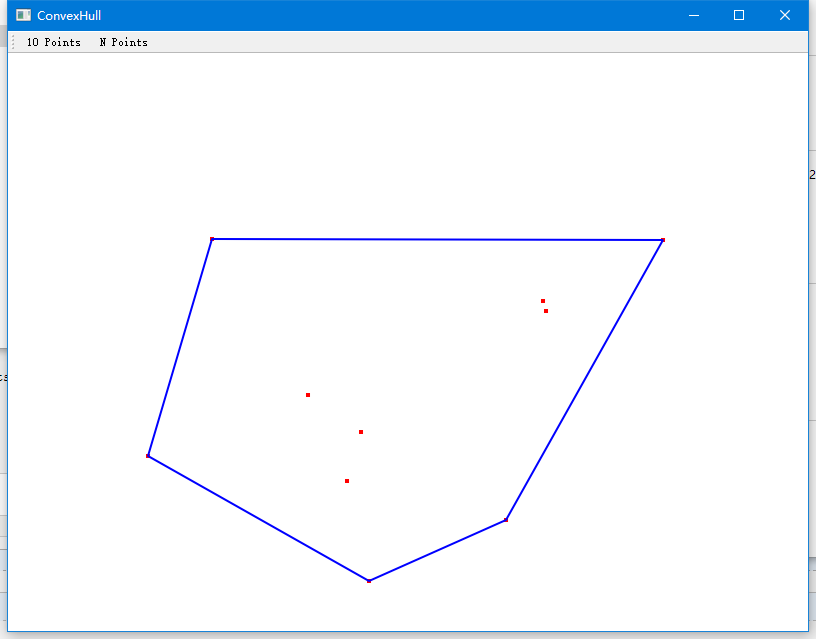
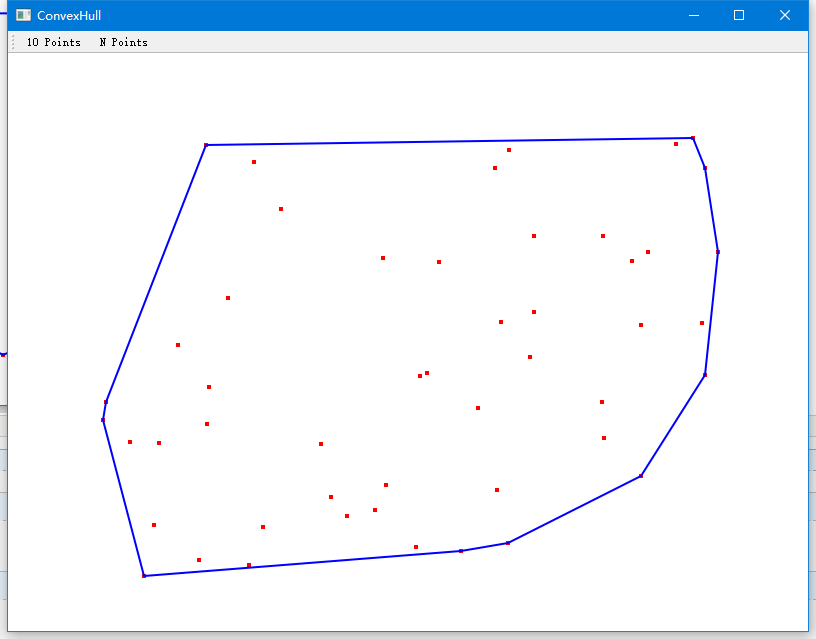
效果如下：

 

程序源码：http://files.cnblogs.com/files/HolyChen/ConvexHull.rar