LibTorch 自动微分

得益于反向传播算法，神经网络计算导数时非常方便，下面代码中演示如何使用LibTorch进行自动微分求导。

进行自动微分运算需要调用函数

torch::autograd::grad(
    outputs,     // 为某个可微函数的输出 y=f(x) 中的 y
    inputs,      // 为某个可微函数的输入 y=f(x) 中的 x
    grad_outputs,// 雅克比矩阵（此处计算 f'(x)，故设置为1，且与x形状相同 ）
    retain_graph,// 默认值与 create_graph 相同，这里设置为 true即可
    create_graph,// 需要设置为 true 以计算高阶导数
    allow_unused // 设置为 false 即可
)

在本文示例中，我们计算 \(y=x^2+x\) 在 \(x = 0.1, 0.3, 0.5\) 处的函数值、一阶导数和二阶导数值，根据我们学到的数学知识，很容易计算出下列数据

\(x\)	0.1	0.3	0.5
\(y\)	0.11	0.39	0.75
\(y'\)	1.20	1.60	2.00
\(y''\)	2.00	2.00	2.00

而在LibTorch中调用自动微分计算导数的代码如下所示

#include <iostream>
#include <torch/torch.h>

int main(int argc, char* atgv[])
{
    std::cout.setf(std::ios::scientific);
    std::cout.precision(7);

    std::vector<float> vec{0.1, 0.3, 0.5};
    torch::Tensor x = torch::from_blob(vec.data(), {3}, torch::kFloat).requires_grad_(true);
    torch::Tensor y = x * x + x; // y= x^2 + x
    auto weight     = torch::ones_like(x);

    std::cout << "x      = ";
    for (int i = 0; i < 3; ++i)
        std::cout << x[i].item<float>() << " ";
    std::cout << std::endl;

    std::cout << "y      = "; // 0.11 0.39 0.75
    for (int i = 0; i < 3; ++i)
        std::cout << y[i].item<float>() << " ";
    std::cout << std::endl;

    // 计算输出一阶导数（y' = 2x + 1）
    auto dydx = torch::autograd::grad({y}, {x}, {weight}, true, true, false);
    std::cout << "dydx   = "; // 1.2 1.6 2.0
    for (int i = 0; i < 3; ++i)
        std::cout << dydx[0][i].item<float>() << " ";
    std::cout << std::endl;

    // 计算输出二阶导数（y''= 2）
    auto d2ydx2 = torch::autograd::grad({dydx[0]}, {x}, {weight});
    std::cout << "d2ydx2 = "; // 2.0 2.0 2.0
    for (int i = 0; i < 3; ++i)
        std::cout << d2ydx2[0][i].item<float>() << " ";
    std::cout << std::endl;

    return 0;
}

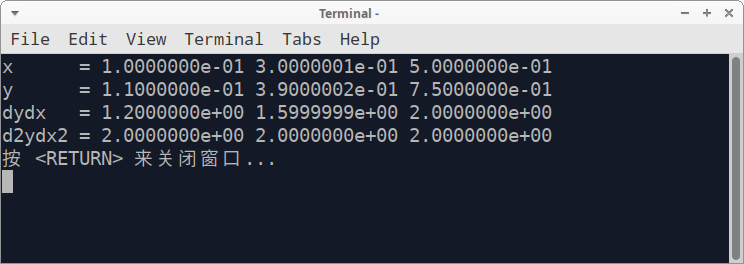
计算结果如下图所示，与我们手动计算的结果一致。