基于python的数学建模---轮廓系数的确定

直接上代码

from sklearn import metrics
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn import preprocessing
import pandas as pd

data = pd.read_csv('tae.csv')
info_scaled = preprocessing.scale(data)
X = info_scaled
score = []
for i in range(2, 18):
    km = KMeans(n_clusters=i, init='k-means++', n_init=10, max_iter=300, random_state=0)
    km.fit(X)
    score.append(metrics.silhouette_score(X, km.labels_, metric='euclidean'))
plt.figure(dpi=150)
plt.plot(range(2, 18), score, marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('silhouette_score')
plt.show()

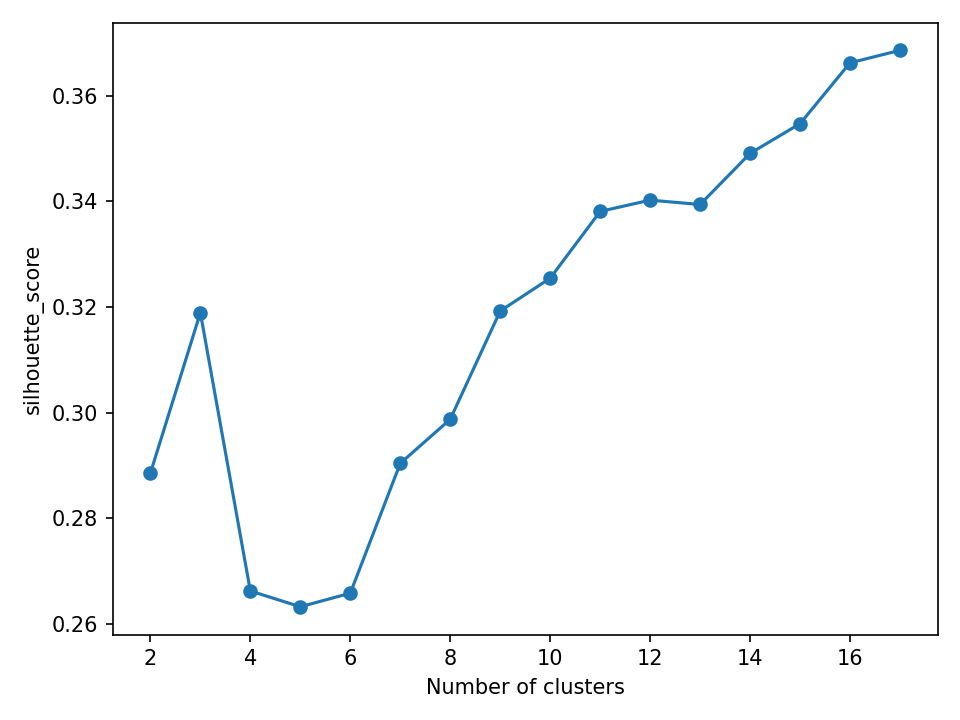
点越高，结果就越准确