岭回归和LASSO
0、对于正则罚项的理解

1、岭回归(L2 ridge regression )
是一种专用于共线性数据分析的有偏估计回归方法,实质上是一种改良的最小二乘估计法,通过放弃最小二乘法的无偏性,以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法,对病态数据的拟合要强于最小二乘法。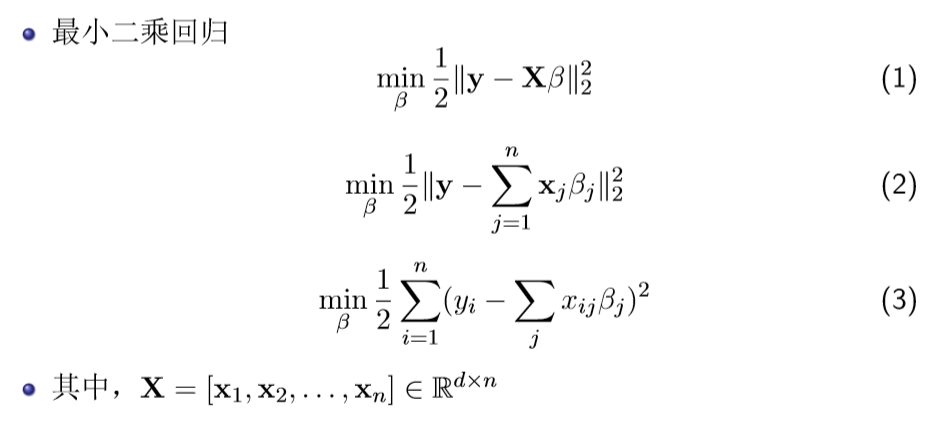

关于最小二乘以及岭回归问题的解:

2、LASSO(Least Absolute Shrinkage and Selection Operator)
该方法是一种压缩估计。它通过构造一个惩罚函数得到一个较为精炼的模型,使得它压缩一些回归系数,即强制系数绝对值之和小于某个固定值;同时设定一些回归系数为零。因此保留了子集收缩的优点,是一种处理具有复共线性数据的有偏估计。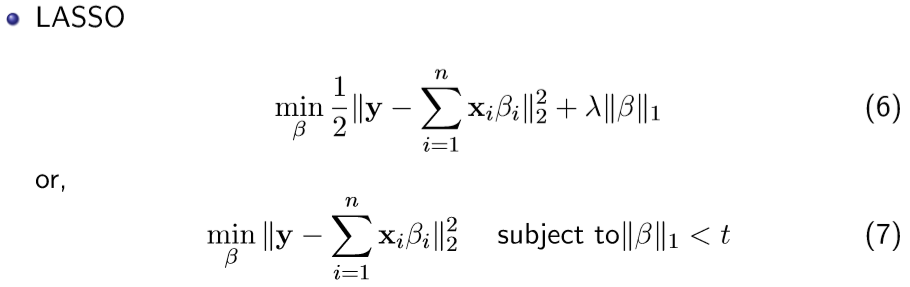


岭回归和LASSO的更多相关文章
- 多重共线性的解决方法之——岭回归与LASSO
多元线性回归模型 的最小二乘估计结果为 如果存在较强的共线性,即 中各列向量之间存在较强的相关性,会导致的从而引起对角线上的 值很大 并且不一样的样本也会导致参数估计值变化非常大.即参数估 ...
- 多元线性回归模型的特征压缩:岭回归和Lasso回归
多元线性回归模型中,如果所有特征一起上,容易造成过拟合使测试数据误差方差过大:因此减少不必要的特征,简化模型是减小方差的一个重要步骤.除了直接对特征筛选,来也可以进行特征压缩,减少某些不重要的特征系数 ...
- 【机器学习】正则化的线性回归 —— 岭回归与Lasso回归
注:正则化是用来防止过拟合的方法.在最开始学习机器学习的课程时,只是觉得这个方法就像某种魔法一样非常神奇的改变了模型的参数.但是一直也无法对其基本原理有一个透彻.直观的理解.直到最近再次接触到这个概念 ...
- 岭回归和Lasso回归以及norm1和norm2
norm代表的是距离,两个向量的距离:下图代表的就是p-norm,其实是对向量里面元素的一种运算: 最简单的距离计算(规范)是欧式距离(Euclidean distance),两点间距离是如下来算的, ...
- 岭回归和lasso回归(转)
回归和分类是机器学习算法所要解决的两个主要问题.分类大家都知道,模型的输出值是离散值,对应着相应的类别,通常的简单分类问题模型输出值是二值的,也就是二分类问题.但是回归就稍微复杂一些,回归模型的输出值 ...
- 岭回归与Lasso回归
线性回归的一般形式 过拟合问题及其解决方法 问题:以下面一张图片展示过拟合问题 解决方法:(1):丢弃一些对我们最终预测结果影响不大的特征,具体哪些特征需要丢弃可以通过PCA算法来实现:(2):使用正 ...
- 机器学习-正则化(岭回归、lasso)和前向逐步回归
机器学习-正则化(岭回归.lasso)和前向逐步回归 本文代码均来自于<机器学习实战> 这三种要处理的是同样的问题,也就是数据的特征数量大于样本数量的情况.这个时候会出现矩阵不可逆的情况, ...
- 岭回归、lasso
参考:https://blog.csdn.net/Byron309/article/details/77716127 ---- https://blog.csdn.net/xbinwor ...
- 机器学习之五 正则化的线性回归-岭回归与Lasso回归
机器学习之五 正则化的线性回归-岭回归与Lasso回归 注:正则化是用来防止过拟合的方法.在最开始学习机器学习的课程时,只是觉得这个方法就像某种魔法一样非常神奇的改变了模型的参数.但是一直也无法对其基 ...
- 【笔记】模型泛化与岭回归与LASSO
模型泛化与岭回归与LASSO 模型正则化 模型正则化,简单来说就是限制参数大小 模型正则化是用什么思路来解决先前过拟合的由于过于拟合导致的曲线抖动(线性方程前的系数都很大) 线性回归的目标就是求一个最 ...
随机推荐
- 甲骨文严查Java授权,换openJDK要避坑
背景 外媒The Register报道,甲骨文稽查企业用户,近期开始将把过去看管较松散的Java授权加入. 甲骨文针对标准版Java(Java SE)有2种商业授权.2019年4月甲骨文宣布Java ...
- 关于在PyCharm中import numpy 出现from . import _mklinit ImportError: DLL load failed: 找不到指定模块
最近因为一些原因安装了Anaconda3并且重新配置Python环境,但是遇到了一些麻烦的事情. 首先就是在Anaconda已经装好numpy和mkl的情况下,在PyCharm中import nump ...
- liunx对磁盘进行配额限制
说明,我们给你一个分区进行磁盘配额进行限制 1.首先我们要进行那个分区进行限制,通过修改配置文件加上uquota ,然后再重启一下系统 二.quota 命令用于管理设备的磁盘容量配额,语法格式为 xf ...
- [AcWing 800] 数组元素的目标和
点击查看代码 #include<iostream> using namespace std; const int N = 1e5 + 10; int a[N], b[N]; int mai ...
- 简述 private、protected、 public、 internal修饰符的访问权限
1.private: 私有的,只能在此类中访问 2.protected: 受保护的,只能在此类及其继承类中访问 3.public: 公开的,没有访问限制 4:internal: 内部的,只能在当前程序 ...
- 通过Go实现AES加密和解密工具
本文包含如下两个内容: AES加密介绍及实现原理 Go实现AES加密和解密工具 AES加密介绍及实现原理 AES( advanced encryption standard)使用相同密钥进行加密和解密 ...
- Bert不完全手册5. 推理提速?训练提速!内存压缩!Albert
Albert是A Lite Bert的缩写,确实Albert通过词向量矩阵分解,以及transformer block的参数共享,大大降低了Bert的参数量级.在我读Albert论文之前,因为Albe ...
- Java学习,利用IDEA开发工具连接redis
Idea连接redis及Jedis数据操作 注意是否开启了redis服务!!! 1.打开虚拟机终端,查看虚拟机防火墙是否关闭 查看防火墙当前状态命令: $sudo ufw status 我的是默认关闭 ...
- Java synchronized那点事
前言 请看上篇:Java 对象头那点事 文章中的源码都有不同程度缩减,来源于openjdk8的开源代码(tag:jdk8-b120). 锁粗化过程 偏向锁 ①:markword中保存的线程ID是自己且 ...
- K8S 使用Kubeadm搭建高可用Kubernetes(K8S)集群 - 证书有效期100年
1.概述 Kubenetes集群的控制平面节点(即Master节点)由数据库服务(Etcd)+其他组件服务(Apiserver.Controller-manager.Scheduler...)组成. ...
